Actually, Othello-GPT Has A Linear Emergent World Representation

Written By Neel Nanda

Othello-GPT

Epistemic Status: This is a write-up of an experiment in speedrunning research, and the core results represent ~20 hours/2.5 days of work (though the write-up took way longer). I'm confident in the main results to the level of "hot damn, check out this graph", but likely have errors in some of the finer details.

Disclaimer: This is a write-up of a personal project, and does not represent the opinions or work of my employer

This post may get heavy on jargon. I recommend looking up unfamiliar terms in my mechanistic interpretability explainer

Thanks to Chris Olah, Martin Wattenberg, David Bau and Kenneth Li for valuable comments and advice on this work, and especially to Kenneth for open sourcing the model weights, dataset and codebase, without which this project wouldn't have been possible!

Overview

  • Context: A recent paper trained a model to play legal moves in Othello by predicting the next move, and found that it had spontaneously learned to compute the full board state - an emergent world representation.
    • This could be recovered by non-linear probes but not linear probes.
    • We can causally intervene on this representation to predictably change model outputs, so it's telling us something real
  • I find that actually, there's a linear representation of the board state!
    • But that rather than "this cell is black", it represents "this cell has my colour", since the model plays both black and white moves.
    • We can causally intervene with the linear probe, and the model makes legal moves in the new board!
  • This is evidence for the linear representation hypothesis: that models, in general, compute features and represent them linearly, as directions in space! (If they don't, mechanistic interpretability would be way harder)
    • The original paper seemed at first like significant evidence for a non-linear representation - the finding of a linear representation hiding underneath shows the real predictive power of this hypothesis!
  • This (slightly) strengthens the paper's evidence that "predict the next token" transformer models are capable of learning a model of the world.
  • Part 2: There's a lot of fascinating questions left to answer about Othello-GPT - I outline some key directions, and how they fit into my bigger picture of mech interp progress
    • Studying modular circuits: A world model implies emergent modularity - many early circuits together compute a single world model, many late circuits each use it. What can we learn about what transformer modularity looks like, and how to reverse-engineer it?
    • Neuron interpretability and Studying Superposition: Prior work has made little progress on understanding MLP neurons. I think Othello GPT's neurons are tractable to understand, yet complex enough to teach us a lot!
    • A transformer circuit laboratory: More broadly, the field has a tension between studying clean, tractable yet over-simplistic toy models and studying the real yet messy problem of interpreting LLMs - Othello-GPT is toy enough to be tractable yet complex enough to be full of mysteries, and I detail many more confusions and conjectures that it could shed light on.
  • Part 3: Reflections on the research process
    • I did the bulk of this project in a weekend (~20 hours total), as a (shockingly successful!) experiment in speed-running mech interp research.
    • I give a detailed account of my actual research process: how I got started, what confusing intermediate results look like, and decisions made at each point
    • I give some process-level takeaways on doing research well and fast.
  • See the accompanying colab notebook and codebase to build on the many dangling threads!

Table of Contents

Introduction

This piece spends a while on discussion, context and takeaways. If you're familiar with the paper skip to my findings, skip to takeaways for my updates from this, and if you want technical results skip to probing

Emergent World Representations is a fascinating recent ICLR Oral paper from Kenneth Li et al, summarised in Kenneth's excellent post on the Gradient. They trained a model (Othello-GPT) to play legal moves in the board game Othello, by giving it random games (generated by choosing a legal next move uniformly at random) and training it to predict the next move. The headline result is that Othello-GPT learns an emergent world representation - despite never being explicitly given the state of the board, and just being tasked to predict the next move, it learns to compute the state of the board at each move. (Note that the point of Othello-GPT is to play legal moves, not good moves, though they also study a model trained to play good moves.)

They present two main pieces of evidence. They can extract the board state from the model's residual stream via non-linear probes (a two layer ReLU MLP). And they can use the probes to causally intervene and change the model's representation of the board (by using gradient descent to have the probes output the new board state) - the model now makes legal moves in the new board state even if they are not legal in the old board, and even if that board state is impossible to reach by legal play!

I've strengthened their headline result by finding that much of their more sophisticated (and thus potentially misleading) techniques can be significantly simplified. Not only does the model learn an emergent world representation, it learns a linear emergent world representation, which can be causally intervened on in a linear way! But rather than representing "this square has a black/white piece", it represents "this square has my/their piece". The model plays both black and white moves, so this is far more natural from its perspective. With this insight, the whole picture clarifies significantly, and the model becomes far more interpretable!

Background

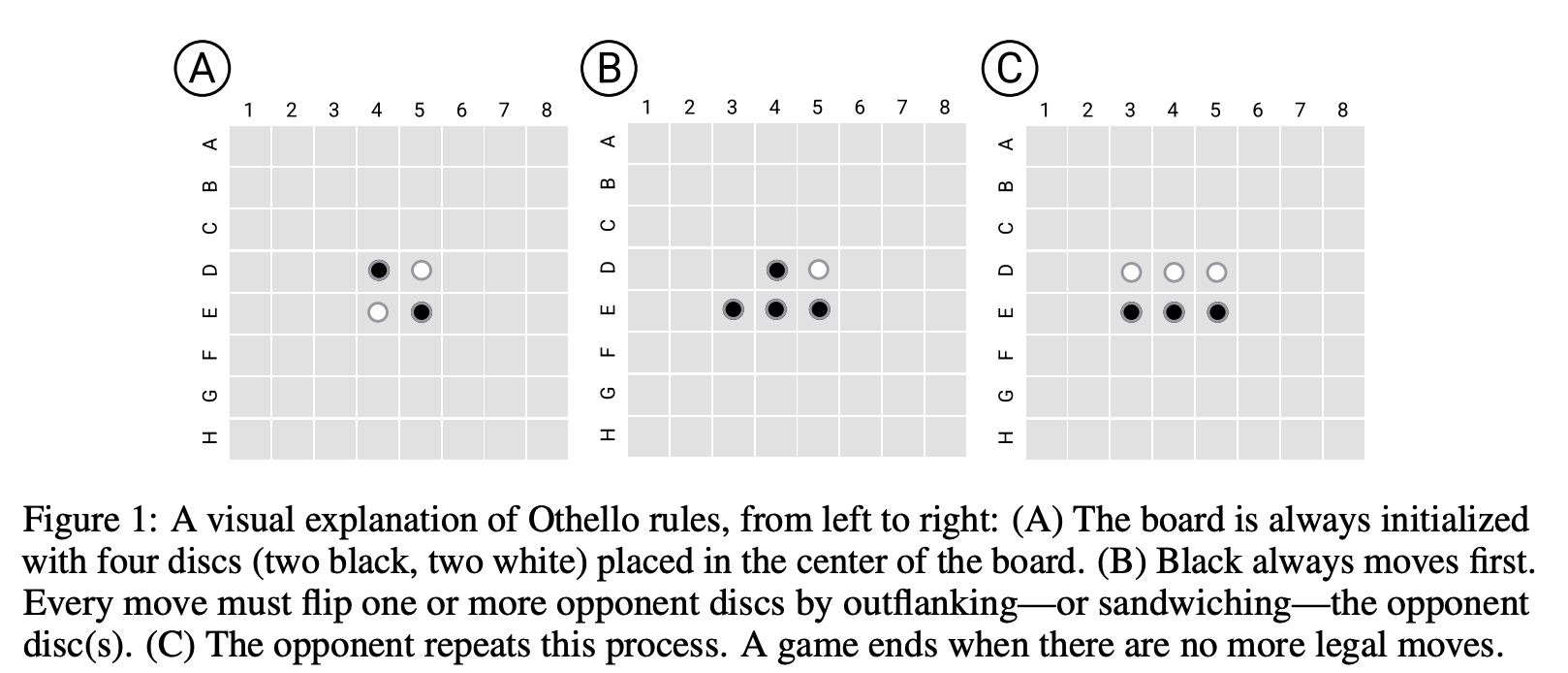
For those unfamiliar, Othello is a board game analogous to chess or go, with two players, black and white, see the rules outlined in the figure below. I found playing the AI on eOthello helpful for building intuition. A single move can change the colour of pieces far away (so long as there's a continuous vertical, horizontal or diagonal line), which means that calculating board state is actually pretty hard! (to my eyes much harder than in chess)

But despite the model just needing to predict the next move, it spontaneously learned to compute the full board state at each move - a fascinating result. A pretty hot question right now is whether LLMs are just bundles of statistical correlations or have some real understanding and computation! This gives suggestive evidence that simple objectives to predict the next token can create rich emergent structure (at least in the toy setting of Othello). Rather than just learning surface level statistics about the distribution of moves, it learned to model the underlying process that generated that data. In my opinion, it's already pretty obvious that transformers can do something more than statistical correlations and pattern matching, see eg induction heads, but it's great to have clearer evidence of fully-fledged world models!

For context on my investigation, it's worth analysing exactly the two pieces of evidence they had for the emergent world representation, the probes and the causal interventions, and their strengths and weaknesses.

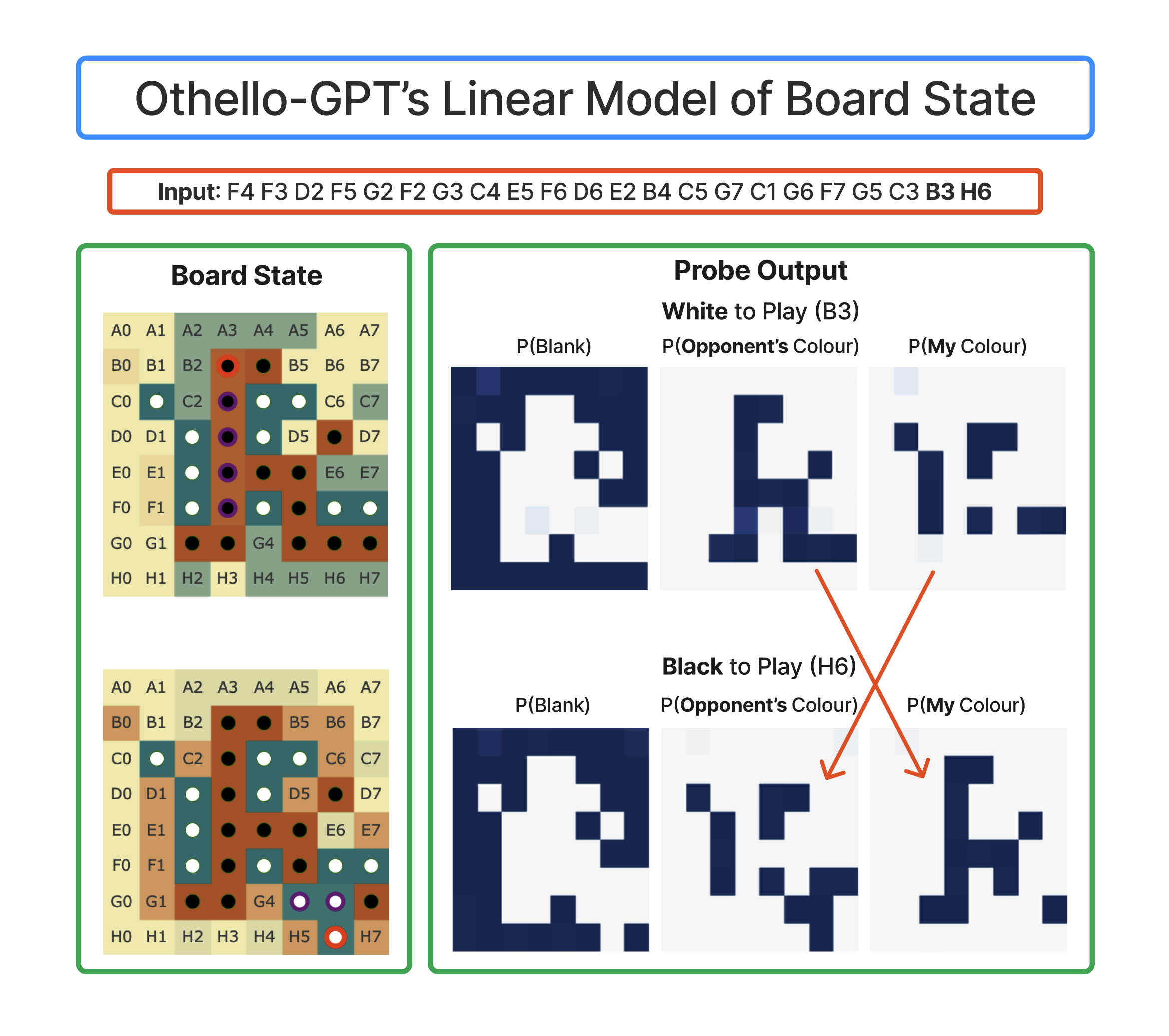
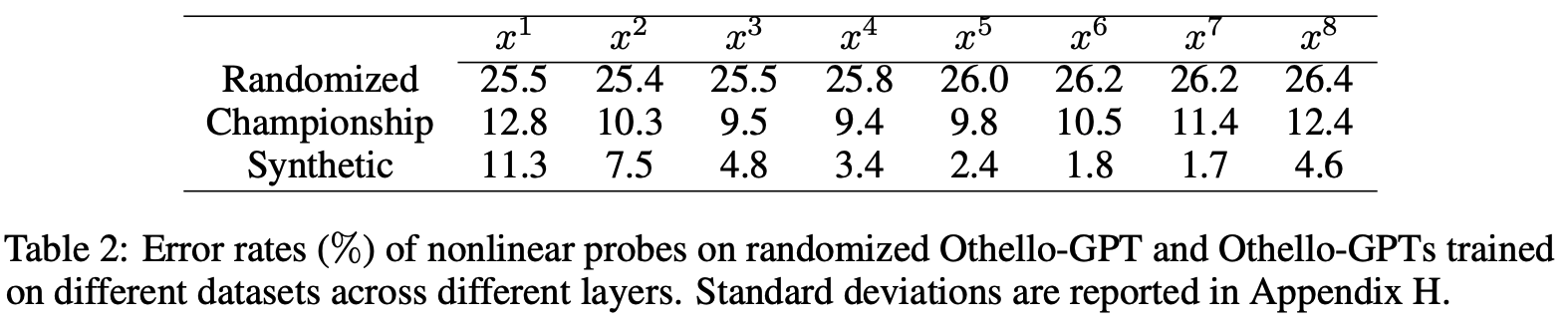
The probes give suggestive, but far from conclusive evidence. When training a probe to extract some feature from a model, it's easy to trick yourself. It's crucial to track whether the probe is just reading out the feature, or actually computing the feature itself, and reading out much simpler features from the model. In the extreme case, you could attach a much more powerful model as your "probe", and have it just extract the input moves, and then compute the board state from scratch! They found that linear probes did not work to recover board state (with an error rate of 20.4%): (ie, projecting the residual stream onto some 3 learned directions for each square, corresponding to empty, black and white logits). While the simplest non-linear probes (a two layer MLP with a single hidden ReLU layer) worked extremely well (an error rate of 1.7%). Further (as described in their table 2, screenshot below), these non-linear probes did not work on a randomly initialised network, and worked better on some layers than others, suggesting they were learning something real from the model.

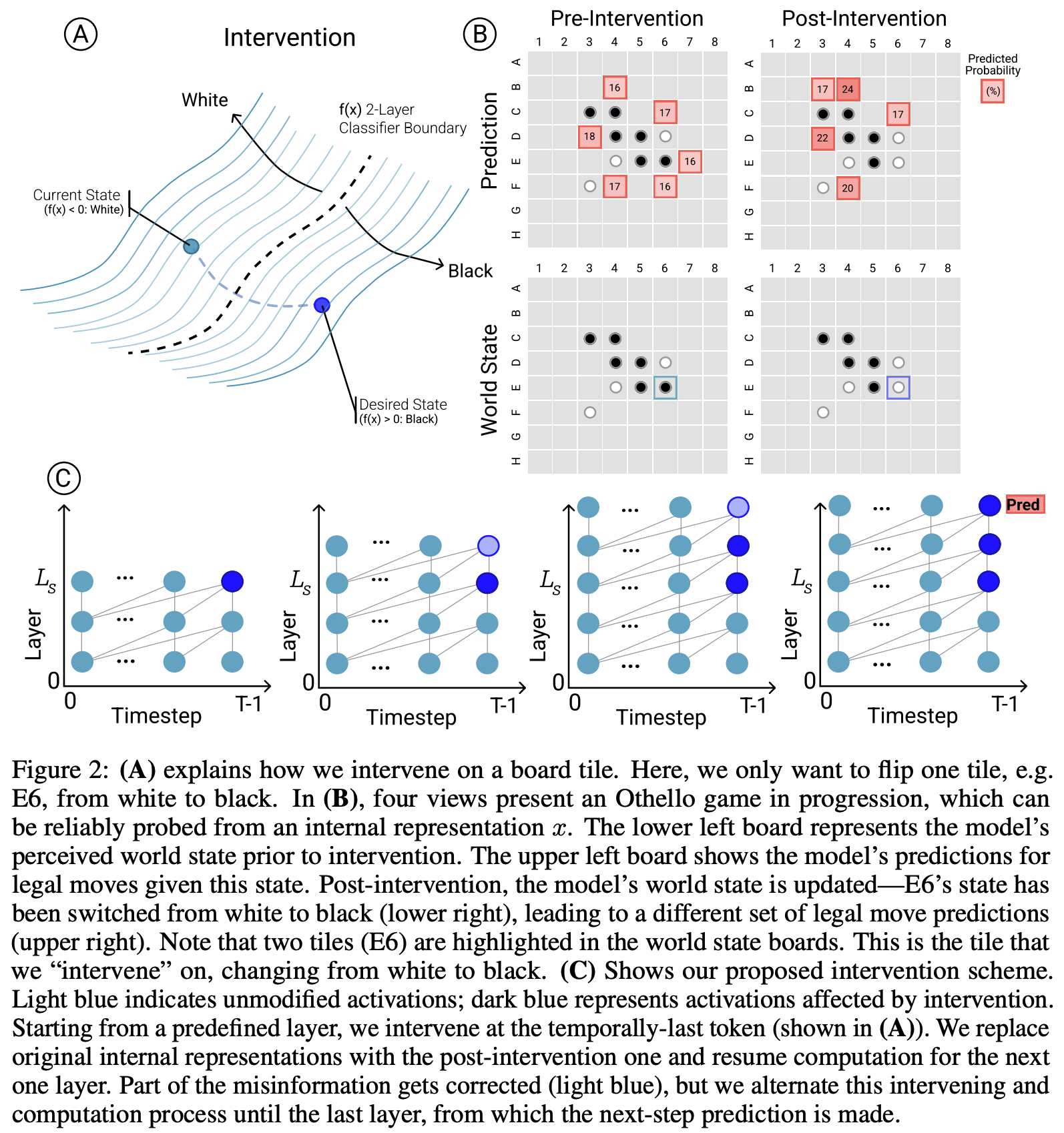
Probes on their own can mislead, and don't necessarily tell us that the model uses this representation - the probe could be extracting some vestigial features or a side effect of some more useful computation, and give a misleading picture of how the model computes the solution. But their causal interventions make this much more compelling evidence. They intervene by a fairly convoluted process (detailed in the figure below, though you don't need to understand the details), which boils down to choosing a new board state, and applying gradient descend to the model's residual stream such that our probe thinks the model's residual stream represents the new board state. I have an immediate skepticism of any complex technique like this: when applying a powerful method like gradient descent it's so easy to wildly diverge from what the models original functioning is like! But the fact that the model could do the non-trivial computation of converting an edited board state into a legal move post-edit is a very impressive result! I consider it very strong evidence both that the probe has discovered something real, and that the representation found by the probe is causally linked to the model's actual computation!

Naive Implications for Mechanistic Interpretability

I was very interested in this paper, because it simultaneously had the fascinating finding of an emergent world model (and I'm also generally into any good interp paper), yet something felt off. The techniques used here seemed "too" powerful. The results were strong enough that something here seemed clearly real, but my intuition is that if you've really understood a model's internals, you should just be able to understand and manipulate it with far simpler techniques, like linear probes and interventions, and it's easy to be misled by more powerful techniques.

In particular, my best guess about model internals is that the networks form decomposable, linear representations: that the model computes a bunch of useful features, and represents these as directions in activation space. See Toy Models of Superposition for some excellent exposition on this. This is decomposable because each feature can vary independently (from the perspective of the model - on the data distribution they're likely dependent), and linear because we can extract a feature by projecting onto that feature's direction (if the features are orthogonal - if we have something like superposition it's messier). This is a natural way for models to work - they're fundamentally a series of matrix multiplications with some non-linearities stuck in convenient places, and a decomposable, linear representation allows it to extract any combination of features with a linear map!

Under this framework, if a feature can be found by a linear probe then the model has already computed it, and if that feature is used in a circuit downstream, we should be able to causally intervene with a linear intervention, just changing the coordinate along that feature's direction. So the fascinating finding that linear probes do not work, but non-linear probes do, suggests that either the model has a fundamentally non-linear representation of features (which it is capable of using directly for downstream computation!), or there's a linear representation of simpler and more natural features, from which the probe computes board state. My prior was on a linear representation of simpler features, but the causal intervention findings felt like moderate evidence for the non-linear representation. And the non-linear representation hypothesis would be a big deal if true! If you want to reverse-engineer a model, you need to have a crisp picture of how its computation maps onto activations and weights, and this would break a lot of my beliefs about how this correspondance works! Further, linear representations are just really convenient to reverse-engineer, and this would make me notably more pessimistic about mechanistic interpretability working.

My Findings

I'm of the opinion that the best way to become less confused about a mysterious model behaviour is to mechanistically analyse it. To zoom in on whatever features and circuits we can find, build our understanding from the bottom up, and use this to form grounded beliefs about what's actually going on. This was the source of my investigation into grokking, and I wanted to apply it here. I started by trying activation patching and looking for interpretable circuits/neurons, and I noticed a motif whereby some neurons would fire every other move, but with different parity each game. Digging further, I stumbled upon neuron 1393 in layer 5, which seemed to learn (D1==white) AND (E2==black) on odd moves, and (D1==black) AND (E2==white) on even moves.

Generalising from this motif, I found that, in fact, the model does learn a linear representation of board state! But rather than having a direction saying eg "square F5 has a black counter" it says "square F5 has one of my counters". In hindsight, thinking in terms of my vs their colour makes far more sense from the model's perspective - it's playing both black and white, and the valid moves for black become valid moves for white if you flip every piece's colour! (I've since this same observation in Haoxing Du's analysis of Go playing models)

If you train a linear probe on just odd/even moves (ie with black/white to play) then it gets near perfect accuracy! And it transfers reasonably well to the other moves, if you flip its output.

I speculate that their non-linear probe just learned to extract the two features of "I am playing white" and "this square has my colour" and to do an XOR of those. Fascinatingly, without the insight to flip every other representation, this is a pathological example for linear probes - the representation flips positive to negative every time, so it's impossible to recover the true linear structure!

And we can use our probe to causally intervene on the model. The first thing I tried was just negating the coordinate in the direction given by the probe for a square (on the residual stream after layer 4, with no further intervention), and it just worked - see the figure below! Note that I consider this the weakest part of my investigation - on further attempts it needs some hyper-parameter fiddling and is imperfect, discussed later, and I've only looked at case studies rather than a systematic benchmark.

This project was an experiment in speed-running mech interp research, and I got all of the main results in this post over a weekend (~2.5 days/20 hours). I am very satisfied with the results of this experiment! I discuss some of my process-level takeaways, and try to outline the underlying research process in a pedagogical way - how I got started, how I got traction on the problem, and what the compelling intermediate results looked like.

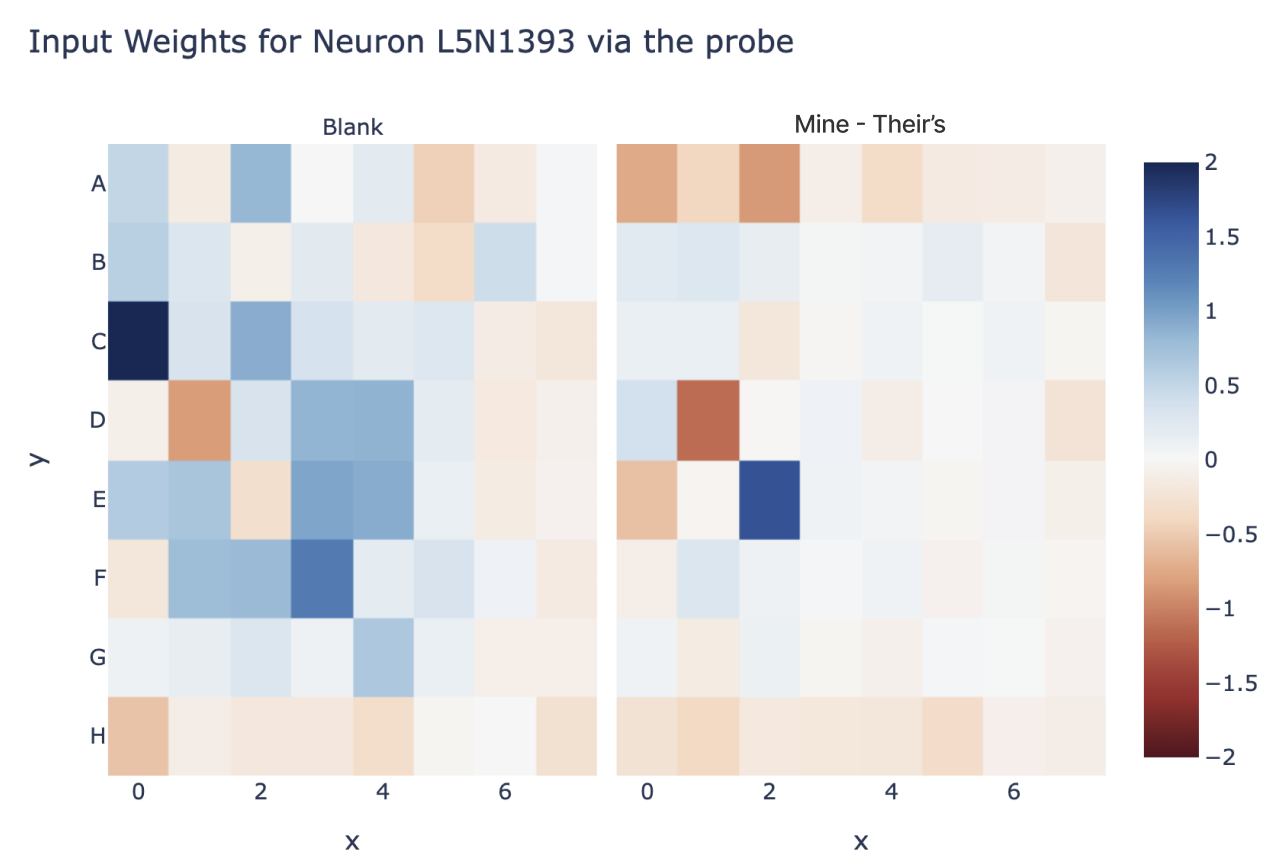
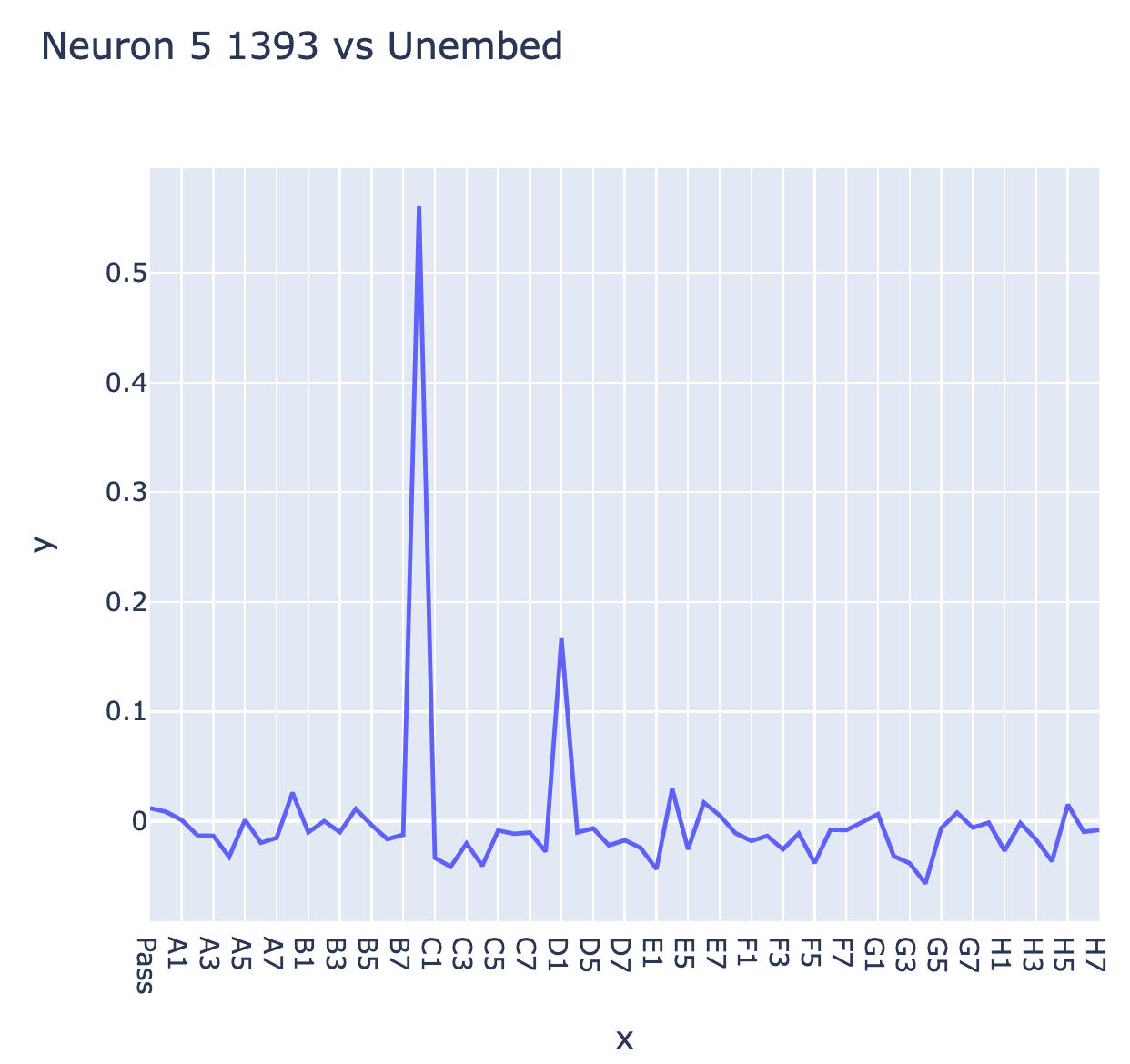
I also found a lot of tantalising hints of deeper structure inside the model! For example, we can use this probe to interpret input and output weights of neurons, eg Neuron 1393 in Layer 5 which seems to represent (C0==blank) AND (D1==theirs) AND (E2==mine) (we convert the probe to two directions, blank - 0.5 * my - 0.5 * their, and my - their)

Or, if we look at the top 1% of dataset examples for some layer 4 neurons and look at the frequency by which a square is non-empty, many seem to activate when a specific square is empty! (But some neighbours are present)

I haven't looked hard into these, but I think there's a lot of exciting directions to better understand this model, that I outline in future work. An angle I'm particularly excited about here is moving beyond just studying "end-to-end" transformer circuits - existing work (eg indirect object identification or induction heads) tends to focus on a circuit that goes from the input tokens to the output logits, because it's much easier to interpret the inputs and outputs than any point in the middle! But our probe can act as a "checkpoint" in the middle - we understand what the probe's directions mean, and we can use this to find early circuits mapping the input moves to compute the world model given by the probe, and late circuits mapping the world model to the output logits!

More generally, the level of traction I've gotten suggests there's a lot of low hanging fruit here! I think this model could serve as an excellent laboratory to test other confusions and claims about models - it's simultaneously clean and algorithmic enough to be tractable, yet large and complex enough to be exciting and less toy. Can we find evidence of superposition? Can we find monosemantic neurons? Are all neurons monosemantic, or can we find and study polysemanticity and superposition in the wild? How do different neuron activations (GELU, SoLU, SwiGLU, etc) affect interpretability? More generally, what kinds of circuits can we find?!

Takeaways

How do models represent features?

My most important takeaway is that this gives moderate evidence for models, in practice, learning decomposable, linear representations! (And I am very glad that I don't need to throw away my frameworks for thinking about models.) Part of the purpose of writing such a long background section is to illustrate that this was genuinely in doubt! The fact that the original paper needed non-linear probes, yet could causally intervene via the probes, seemed to suggest a genuinely non-linear representation, and this could have gone either way. But I now know (and it may feel obvious in hindsight) that it was linear.

As further evidence that this was genuinely in doubt, I've since become aware of an independent discussion between Chris Olah and Martin Wattenberg (an author of the paper), where I gather that Chris pre-registered the prediction that the probe was doing computation on an underlying linear representation, while Martin thought the model learned a genuinely non-linear representation.

Models are complex and we aren't (yet!) very good at reverse-engineering them, which makes evidence for how best to think about them sparse and speculative. One of the best things we have to work with is toy models that are complex enough that we don't know in advance what gradient descent will learn, yet simple enough that we can in practice reverse-engineer them, and Othello-GPT formed an unexpectedly pure natural experiment!

Conceptual Takeaways

A further smattering of conceptual takeaways I have about mech interp from this work - these are fairly speculative, and are mostly just slight updates to beliefs I already held, but hopefully of interest!

An obvious caveat to all of the below is that this is preliminary work on a toy model, and generalising to language models is speculative - Othello is a far simpler environment than language/the real world, a far smaller state space, Othello-GPT is likely over-parametrised for good performance on this task while language models are always under-parametetrised, and there's a ground truth solution to the task. I think extrapolation like this is better than nothing, but there are many disanalogies and it's easy to be overconfident!

  • Mech interp for science of deep learning: A motivating belief for my grokking work is that mechanistic interpretability should be a valuable tool for the science of deep learning. If our claims about truly reverse-engineering models are true, then the mech interp toolkit should give grounded and true beliefs about models. So when we encounter mysterious behaviour in a model, mechanistic analysis should de-mystify it!
    • I feel validated in this belief by the traction I got on grokking, and I feel further validated here!
  • Mech interp == alien neuroscience: A pithy way to describe mech interp is as understanding the brain of an alien organism, but this feels surprisingly validated here! The model was alien and unintuitive, in that I needed to think in terms of my colour vs their colour, not black vs white, but once I'd found this new perspective it all became far clearer and more interpretable.
  • Models can be deeply understood: More fundamentally, this is further evidence that neural networks are genuinely understandable and interpretable, if we can just learn to speak their language. And it makes me mildly more optimistic that narrow investigations into circuits can uncover the underlying principles that will make model internals make sense
    • Further, it's evidence that as you start to really understand a model, mysteries start to dissolve, and it becomes far easier to control and edit - we went from needing to do gradient descent against a non-linear probe to just changing the coordinate along a single direction at a single activation.
  • Probing is surprisingly legit: As noted, I'm skeptical by default about any attempt to understand model internals, especially without evidence from a mechanistically understood case study!
    • Probing, on the face of it, seems like an exciting approach to understand what models really represent, but is rife with conceptual issues:
      • Is the probe computing the feature, or is the model?
      • Is the feature causally used/deliberately computed, or just an accident?
      • Even if the feature does get deliberately computed and used, have we found where the feature is first computed, or did we find downstream features computed from it (and thus correlated with it)
    • I was pleasantly surprised by how well linear probes worked here! I just did naive logistic regression (using AdamW to minimise cross-entropy loss) and none of these issues came up, even though eg some squares had pretty imbalanced class labels.
    • In particular, even though it later turned out that the board state was fully computed by layer 4, and I trained my probe on layer 6, it still picked up on the correct features (allowing intervention at layer 4) - despite the board state being used by layers 5 and 6 to compute downstream features!
  • Dropout => redundancy: Othello-GPT was, alas trained with attention and residual dropout (because it was built on the MinGPT codebase, which was inspired by GPT-2, which used them). Similar to the backup name movers in GPT-2 Small, I found some suggestive evidence of redundancy built into the model - in particular, the final MLP layer seemed to contribute negatively to a particular logit, but would reduce this to compensate when I patched some model internal.
  • Basic techniques just kinda worked?: The main tools I used in this investigation, activation patching, direct logit attribution and max activating dataset examples, basically just worked. I didn't probe hard enough to be confident they didn't mislead me at all, but they all seemed to give me genuinely useful data and hints about model internals.
  • Residual models are ensembles of shallow paths: Further evidence that the residual stream is the central object of a transformer, and the meaningful paths of computation tend not to go through every layer, but heavily use the skip connections. This one is more speculative, but I often noticed that eg layer 3 and layer 4 did similar things, and layer 5 and layer 6 neurons did similar things. (Though I'm not confident there weren't subtle interactions, especially re dropout!)
  • Can LLMs understand things?: A major source of excitement about the original Othello paper was that it showed a predict-the-next-token model spotaneously learning the underlying structure generating its data - the obvious inference is that a large language model, trained to predict the next token in natural language, may spontaneously learn to model the world. To the degree that you took the original paper as evidence for this, I think that my results strengthen the original paper's claims, including as evidence for this!
    • My personal take is that LLMs obviously learn something more than just statistical correlations, and that this should be pretty obvious from interacting with them! (And finding actual inference-time algorithms like induction heads just reinforces this). But I'm not sure how much the paper is a meaningful update for what actually happens in practice.
    • Literally the only thing Othello-GPT cares about is playing legal moves, and having a representation of the board is valuable for that, so it makes sense that it'd get a lot of investment (having 128 probe directions gets you). But likely a bunch of dumb heuristics would be much cheaper and work OK for much worse performance - we see that the model trained to be good at Othello seems to have a much worse world model.
      • Further, computing the board state is way harder than it seems at first glance! If I coded up an Othello bot, I'd have it compute the board state iteratively, updating after each move. But transformers are built to do parallel, not serial processing - they can't recurse! In just 5 blocks, it needs to simultaneously compute the board state at every position (I'm very curious how it does this!)
      • And taking up 2 dimensions per square consumes 128 of the residual stream's 512 dimensions (ignoring any intermediate terms), a major investment!
    • For an LLM, it seems clear that it can learn some kind of world model if it really wants to, and this paper demonstrates that principle convincingly. And it's plausible to me that for any task where a world model would help, a sufficiently large LLM will learn the relevant world model, to get that extra shred of recovered loss. But this is a fundamentally empirical question, and I'd love to see data studying real models!
      • Note further that if an LLM does learn a world model, it's likely just one circuit among many and thus hard to reliably detect - I'm sure it'll be easy to generate gotchas where the LLM violates what that world model says, if only because the LLM wants to predict the next token, and it's easy to cue it to use another circuit. There's been some recent Twitter buzz about Bing Chat playing legal chess moves, and I'm personally pretty agnostic about whether it has a real model of a chess board - it seems hard to say either way (especially when models are using chain of thought for some basic recursion!).
      • One of my hopes is that once we get good enough at mech interp, we'll be able to make confident statements about what's actually going on in situations like this!

Probing

Technical Setup

I use the synthetic model from their paper, and you can check out that and their codebase for the technical details. In brief, it's an 8 layer GPT-2 model, trained on a synthetic dataset of Othello games to predict the next move. The games are length 60, it receives the first 59 moves as input (ie [0:-1]) and it predicts the final 59 moves (ie [1:]). It's trained with attention dropout and residual dropout. The model has vocab size 61 - one for each square on the board (1 to 60), apart from the four center squares that are filled at the start and thus unplayable, plus a special token (0) for passing.

I trained my probe on four million synthetic games (though way fewer would suffice), you can see the training code in tl_probing_v1.py in my repo. I trained a separate probe on even, odd and all moves. I only trained my probe on moves [5:-5] because the model seemed to do weirder things on early or late moves (eg the residual stream on the first move has ~20x the norm of every other one!) and I didn't want to deal with that. I trained them to minimise the cross-entropy loss for predicting empty, black and white, and used AdamW with lr=1e-4, weight_decay=1e-2, eps=1e-8, betas=(0.9, 0.99). I trained the probe on the residual stream after layer 6 (ie get_act_name("resid_post", 6) in TransformerLens notation). In hindsight, I should have trained on layer 6, which is the point where the board state is fully computed and starts to really be used. Note that I believe the original paper trained on the full game (including early and late moves), so my task is somewhat easier than their's.

For each square, each probe has 3 directions, one for blank, black and for white. I convert it to two directions: a "my" direction by taking my_probe = black_dir - white_dir (for black to play) and a "blank" direction by taking blank_probe = blank_dir - 0.5 * black_dir - 0.5 * white_dir (the last one isn't that principled, but it seemed to work fine) (you can throw away the third dimension, since softmax is translation invariant). I then normalise them to be unit vectors (since the norm doesn't matter - it just affects confidence in the probe's logits, which affects loss but not accuracy). I just did this for the black to play probe, and used these as my meaningful directions (this was somewhat hacky, but worked!)

Results

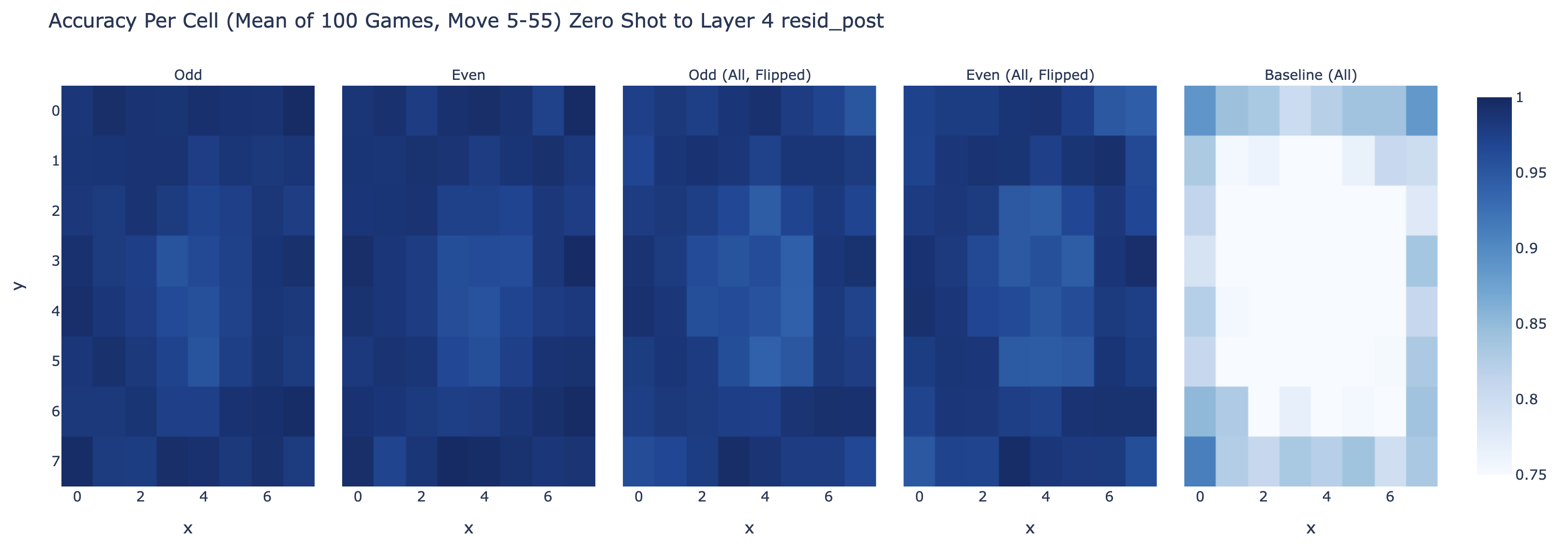
The probe works pretty great for layer 6! And odd (black to play) transfers fairly wel zero shot to even (white to play) by just swapping what mine and your's means (with worse accuracy on the corners). (This is the accuracy taken over 100 games, so 5000 moves, only scored on the middle band of moves)

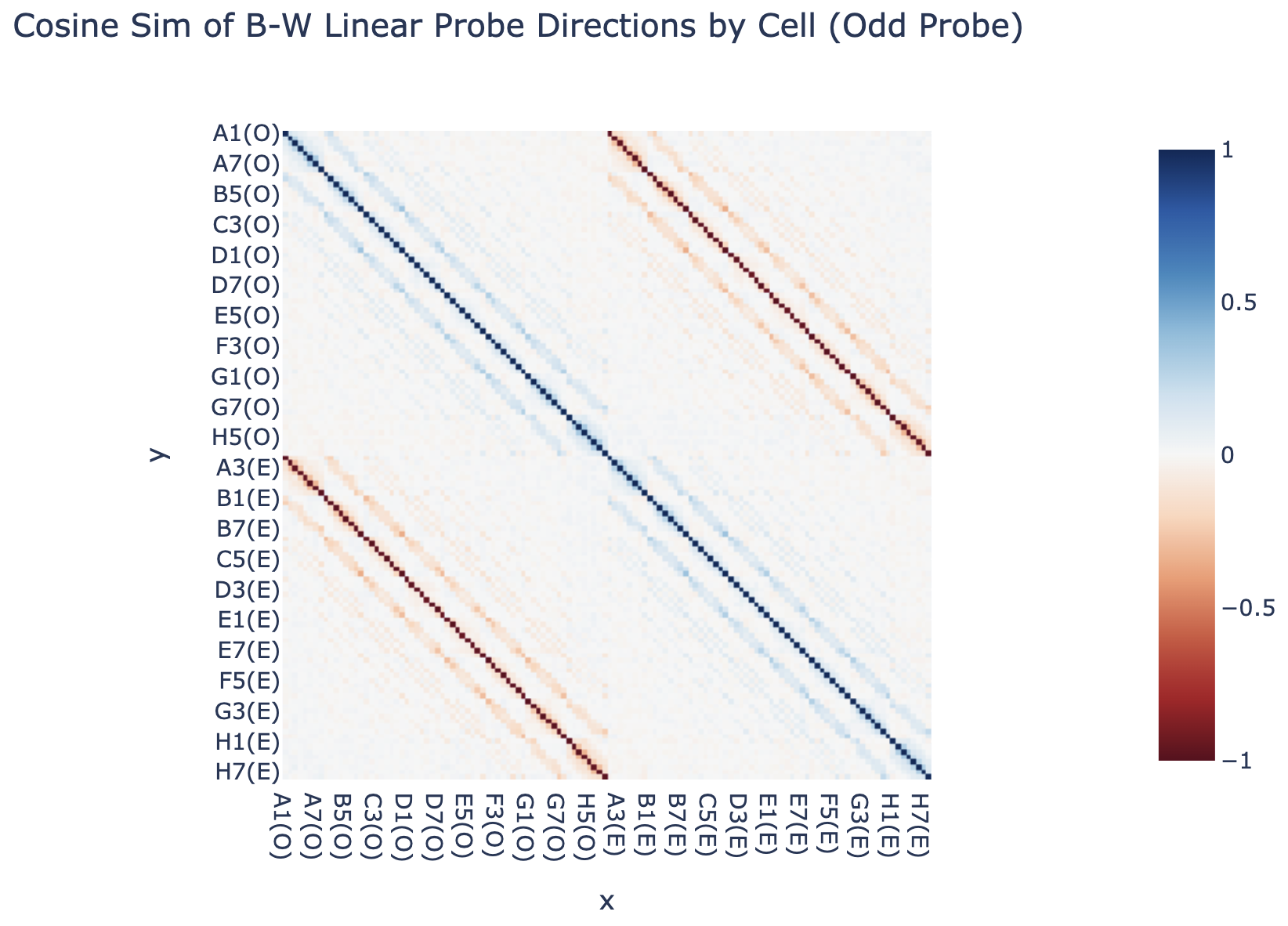
Further, if you flip either probe, it transfers well to the other side's moves, and the odd and even probes are nearly negations of each other. We convert a probe to a direction by taking the difference between the black direction and white direction. (In hindsight, it'd have made been cleaner to train a single probe on all moves, flipped the labels for black to play vs white to play)

It actually transfers zero-shot to other layers - it's pretty great at layer 4 too (but isn't as good at layer 3 or layer 7):

Intervening

My intervention results are mostly a series of case studies, and I think are less compelling and rigorous than the rest, but are strong enough that I buy them! (I couldn't come up with a principled way of evaluating this at scale, and I didn't have much time left). The following aren't cherry picked - they're just the first few things I tried, and all of them kinda worked!

To intervene, I took the model's residual stream after layer 4 (or layer 3), took the coordinate when projecting onto my_probe, and negated that and multiplied by the hyper-parameter scale (which varied from 0 to 16).

My first experiment had layer 4 and scale 1 (ie just negating) and worked pretty well:

Subsequent experiments showed that the scale parameter mattered a fair bit - I speculate that if I instead looked at the absolute coefficient of the coordinate it'd work better.

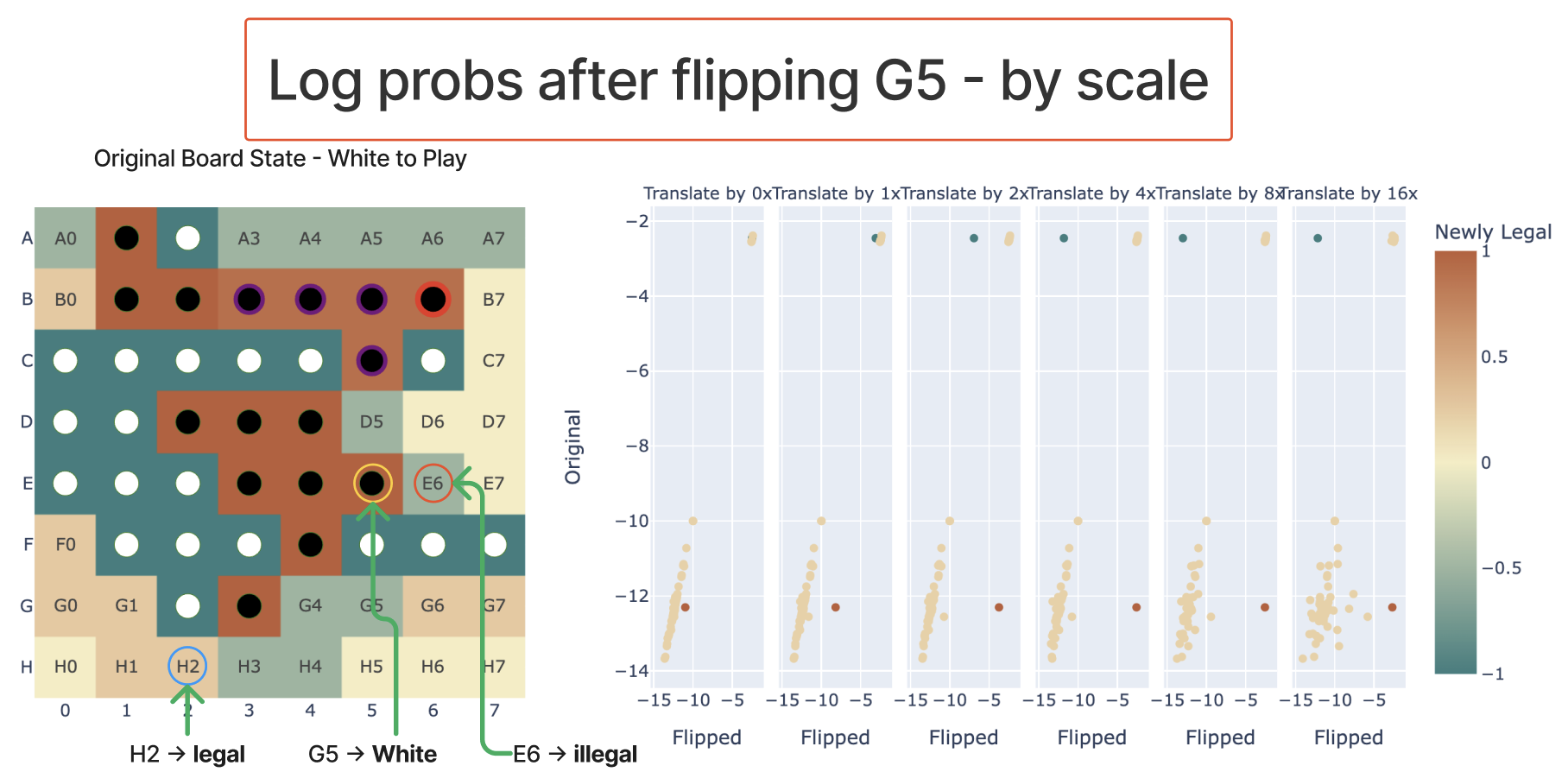
On the first case where it didn't really work, I got good results by intervening at layer 3 instead - evidence that model processing isn't perfectly divided by layer, but somewhat spreads across adjacent layers when it can get away with it.

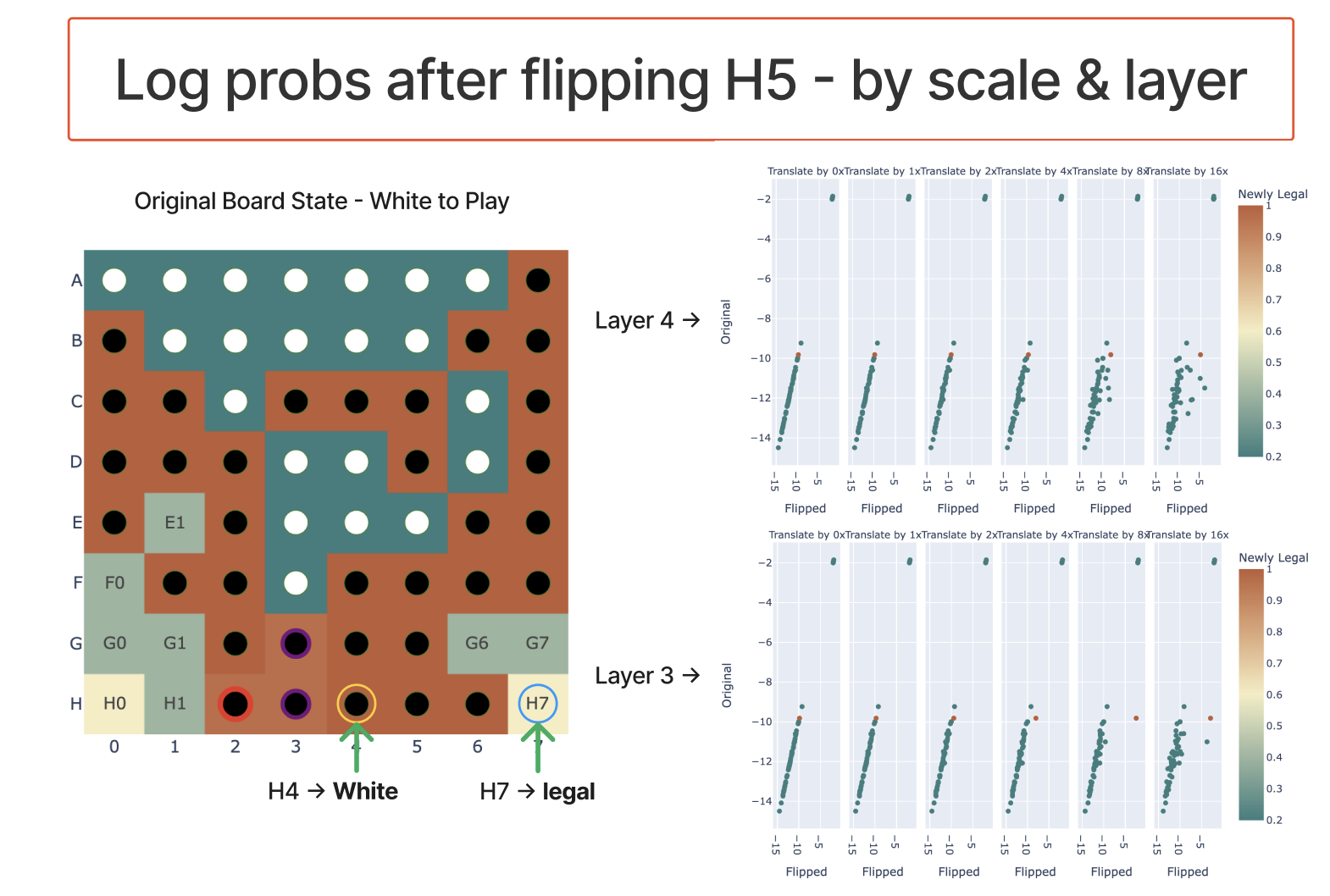
It seems to somewhat work for multiple edits - if I flip F5 and F6 in the above game to make G6 illegal, it kinda realises this, though is a weaker effect and is jankier and more fragile:

Note that my edits do not perfectly recover performance - the newly legal logits tend to not be quite as large as the originally legal logits. To me this doesn't feel like a big deal, here's some takes on why this is fine:

  • I really haven't tried to improve edit performance, and expect there's low hanging fruit to be had. Eg, I train the probe on layer 6 rather than layer 4, and I train on black and white moves separately rather than on both at once. And I am purely scaling the existing coordinate in this direction, rather than looking at its absolute value.
  • Log probs cluster strongly on an unedited game - correct log probs are near exactly the same (around -2 for these games - uniform probability), incorrect log probs tend to be around -11. So even if I get from -11 to -4, that's a major impact
  • I expect parallel model computation to be split across layers - in theory the model could have mostly computed board state by layer 3, use that partial result in layer 4 and finish computing it in layer 4, and use the full result later. If so, then we can't expect to get a perfect model edit.
  • A final reason is that this model was trained with dropout, which makes everything (especially anything to do with model editing) messy. The model has built in redundancy, and likely doesn't have exactly one dimension per feature. (This makes anything to do with patching or editing a bit suspect and unpredictable, unfortunately)

Future work I am excited about

The above sections leaves me (and hopefully you!) pretty convinced that I've found something real and dissolved the mystery of whether there's a linear vs non-linear representation. But I think there's a lot of exciting mysteries left to uncover in Othello-GPT, and that doing so may be a promising way to get better at reverse-engineering LLMs (the goal I actually care about). In the following sections, I try to:

  • Justify why I think further work on Othello-GPT is interesting
  • Discuss how this unlocks finding modular circuits, and some preliminary results
    • Rather than purely studying circuits mapping input tokens to output logits (like basically all prior transformer circuits work), using the probe we can study circuits mapping the input tokens to the world model, and the world model to the output logits - the difference between thinking of a program as a massive block of code vs being split into functions and modules.
    • If we want to reverse-engineer large models, I think we need to get good at this!
  • Discuss how we can interpret Othello-GPT's neurons - we're very bad at interpreting transformer MLP neurons, and I think that Othello-GPT's are simple enough to be tractable yet complex enough to teach us something!
  • Discuss how, more broadly, Othello-GPT can act as a laboratory to get data on many other questions in transformer circuits - it's simple enough to have a ground truth, yet complex enough to be interesting

My hope is that some people reading this are interested enough to actually try working on these problems, and I end this section with advice on where to start.

Why and when to work on toy models

This is a long and rambly section about my research philosophy of mech interp, and you should feel free to move on to the next section if that's not your jam

At first glance, playing legal moves in Othello (not even playing good moves!) has nothing to do with language models, and I think this is a strong claim worth justifying. Can working on toy tasks like Othello-GPT really help us to reverse-engineer LLMs like GPT-4? I'm not sure! But I think it's a plausible bet worth making.

To walk through my reasoning, it's worth first thinking on what's holding us back - why haven't we already reverse-engineered the most capable models out there? I'd personally point to a few key factors (though note that this is my personal hot take, is not comprehensive, and I'm sure other researchers have their own views!):

  • Conceptual frameworks: To reverse-engineer a transformer, you need to know how to think like a transformer. Questions like: What kinds of algorithms is it natural for a transformer to represent, and how? Are features and circuits the right way to think about it? Is it even reasonable to expect that reverse-engineering is possible? How can we tell if a hypothesis or technique is principled vs hopelessly confused? What does it even mean to have truly identified a feature or circuit?
    • I personally thought A Mathematical Framework significantly clarified my conceptual frameworks for transformer circuits!
    • This blog post is fundamentally motivated by forming better conceptual frameworks - do models form linear representations?
  • Practical Knowledge/Techniques: Understanding models is hard, and being able to do this in practice is hard. Getting better at this both looks like forming a better toolkit of techniques that help us form true beliefs about models, and also just having a bunch of practical experience with finding circuits and refining the tools - can we find any cases where they break? How can we best interpret the results?
    • A concrete way this is hard is that models contain many circuits, each of which only activates on certain inputs. To identify a circuit we must first identify where it is and what it does, out of the morass! Activation patching (used in ROME, Interpretability in the Wild and refined with causal scrubbing) is an important innovation here.
  • Understanding MLP Layers: 2/3 of the parameters in transformers are in MLP layers, which process the information collected at each token position. We're pretty bad understanding them, and getting better at this is vital!
    • We think these layers represent features as directions in space, and if each neuron represents a single feature, we're pretty good! But in practice this seems to be false, because of the poorly understood phenomena of superposition and polysemanticity
    • Toy Models of Superposition helped clarify my conceptual frameworks re superposition, but there's still a lot more to de-confuse! And a lot of work to do to form the techniques to deal with it in practice. I'm still not aware of a single satisfying example of really understanding a circuit involving MLPs in a language model
  • Scalability: LLMs are big, and getting bigger all the time. Even if we solve all of the above in eg four layer transformers, this could easily involve some very ad-hoc and labour intensive techniques. Will this transfer to models far larger? And how well do the conceptual frameworks we form transformer - do they just break on models that are much more complex?
    • This often overlaps with forming techniques (eg, causal scrubbing is an automated algorithm with the potential to scale, modulo figuring out many efficiency and implementation details). But broadly I don't see much work on this publicly, and would be excited to see more - in particular, checking how well our conceptual frameworks transfer, and whether all the work on small models is a bit of a waste of time!
      • My personal hot take is that I'm more concerned about never getting really good at interpreting a four layer model, than about scaling if we're really good at four layer models - both because I just feel pretty confused about even small models, and because taking understood yet labour-intensive techniques and making them faster and more automatable seems hard but doable (especially with near-AGI systems!). But this is a complex empirical question and I could easily be wrong.

Within this worldview, what should our research goals be? Fundamentally, I'm an empiricist - models are hard and confusing, it's easy to trick yourself, and often intuitions can mislead. The core thing of any research project is getting feedback from reality, and using it to form true beliefs about models. This can either look like forming explicit hypotheses and testing them, or exploring a model and seeing what you stumble upon, but the fundamental question is whether you have the potential to be surprised and to get feedback from reality.

This means that any project is a trade-off between tractability and relevance to the end goal. Studying toy, algorithmic models is a double edged sword. They can be very tractable: they're clean and algorithmic which incentivises clean circuits, there's an available ground truth for what the model should be doing, and they're often in a simple and nicely constrained domain. But it's extremely easy for them to cease to be relevant to real LLMs and become a nerd-snipe. (Eg, I personally spent a while working on grokking, and while this was very fun, I think it's just not very relevant to LLMs)

It's pretty hard to do research by constantly checking whether you're being nerd-sniped, and to me there are two natural solutions:

  • (1) To pick a concrete question you care about in language models, and to set out to specifically answer that, in a toy model that you're confident is a good proxy for that question
  • (2) To pick a toy model that's a good enough proxy for LLMs in general, and just try hard to get as much traction on reverse-engineering that model as you can.
    • Eg A Mathematical Framework - I think that "train a model exactly like an LLM, but with only 1 or 2 layers" is pretty good as proxies go, though not perfect.

To me, working on Othello-GPT is essentially a bet on (2), that there in gneeral some are underlying principles of transformers and how they learn circuits, and that the way they manifest in Othello-GPT can teach us things about real models. This is definitely wrong in some ways (I don't expect the specific circuits we find to be in GPT-3!), and it's plausible this is wrong in enough ways to be not worth working on, but I think it seems plausible enough to be a worthwhile research direction. My high-level take is just "I think this is a good enough proxy about LLMs that studying it hard will teach us generally useful things".

There's a bunch of key disanalogies to be careful of! Othello is fundamentally not the same task as language: Othello is a much simpler task, there's only 60 moves, there's a rigid and clearly defined syntax with correct and incorrect answers (not a continuous mess), the relevant info about moves so far can be fully captured by the current board state, and generally many sub-tasks in language will not apply.

But it's also surprisingly analogous, at least by the standards of toy models! Most obviously, it's a transformer trained to predict the next token! But the task is also much more complex than eg modular addition, and it has to do it in weird ways! The way I'd code Othello is by doing it recursively - find the board state at move n and use it to get the state at move n+1. But transformers can't do this, they need to do things with a fixed number of serial steps but with a lot of computation in parallel (ie, at every move it must simultaneously compute the board state at that move in parallel) - it's not obvious to me how to do this, and I expect that the way it's encoded will teach me a lot about how to represent certain kinds of algorithms in transformers. And it needs to be solving a bunch of sub-tasks that interact in weird ways (eg, a piece can be taken multiple times in each of four different directions), computing and remembering a lot of information, and generally forming coherent circuits.

In the next few sections I'll argue for how finding modular circuits can help build practical knowledge and techniques, what we could learn from understanding its MLPs, and more broadly how it could act as a laboratory for forming better conceptual frameworks (it's clearly not a good way to study scalability lol)

This is not about world models

A high-level clarification: Though the focus of the original paper was on understanding how LLMs can form emergent world models, this is not why I am arguing for these research directions. My interpretation of the original paper was that it was strong evidence for the fact that it's possible for "predict the next token" models to form world emergent models, despite never having explicit access to the ground truth of the world/board state. I personally was already convinced that this was possible, but think the authors did great work that showed this convincingly and well (and I am even more convinced after my follow-up!), and that there's not much more to say on the "is this possible" question.

There's many interesting questions about whether these happen in practice in LLMs and what this might look like and how to interpret it - my personal guess is that they do sometimes, but are pretty expensive (in terms of parameters and residual stream bandwidth) and only form when it's high value for reducing next token loss and the model is big enough to afford it. Further, there's often much cheaper hacks, eg, BingChat doesn't need to have formed an explicit chess board model to be decent at playing legal moves in chess! Probably not even for reasonably good legal play: the chess board state is way easier than Othello, pieces can't even change colour! And you can get away with an implicit rather than explicit world model that just computes the relevant features from the context, eg to see where to a move a piece from, just look up the most recent point where that piece was played and look at the position it was moved to.

But Othello is very disanalogous to language here - playing legal moves in Othello has a single, perfectly sufficient world model that I can easily code up (though not quite in four transformer layers!), and which is incredibly useful for answering the underlying task! Naively, Othello-GPT roughly seems to be spending 128 of its 512 residual stream dimensions of this model, which is very expensive (though it's probably using superposition). So while it's a proof of concept that world models are possible, I don't think the finer details here tell us much about whether these world models actually happen in real LLMs. This seems best studied by actually looking at language models, and I think there's many exciting questions here! (eg doing mech interp on Patel et al's work) The point of my investigation was more to refine our conceptual frameworks for thinking about models/transformers, and the goal of these proposed directions is to push forward transformer mech interp in general.

Finding Modular Circuits

Basically all prior work on circuits (eg, induction heads, indirect object identification, the docstring circuit, and modular addition) have been on what I call end-to-end circuits. We take some model behaviour that maps certain inputs to certain outputs (eg the input of text with repetition, and the output of logits correctly predicting the repetition), and analyse the circuit going from the inputs to the outputs.

This makes sense as a place to start! The inputs and outputs are inherently interpretable, and the most obvious thing to care about. But it stands in contrast to much of the image circuits work, that identified neurons representing interpretable features (like curves) and studied how they were computed and how these were used to computed more sophisticated features (like car wheels -> cars). Let's consider the analogy of mech interp to reverse-engineering a compiled program binary to source code. End-to-end circuits are like thinking of the source code as a single massive block of code, and identifying which sections we can ignore.

But a natural thing to aim for is to find variables, corresponding to interpretable activations within the network that correspond to features, some property of the input. The linear representation hypothesis says that these should be directions in activation space. It's not guaranteed that LLMs are modular in the sense of forming interpretable intermediate features, but this seems implied by exiasting work, eg in the residual stream (often studied with probes), or in the MLP layers (possibly as interpretable neurons). If we can find interpretable variables, then the reverse-engineering task becomes much easier - we can now separately analyse the circuits that form the feature(s) from the inputs or earlier features, and the circuits that use the feature(s) to compute the output logits or more complex feature.

I call a circuit which starts or ends at some intermediate activation a modular circuit (in contrast to end-to-end circuits). These will likely differ in two key ways from end-to-end circuits:

  • They will likely be shallower, ie involving fewer layers of composition, because they're not end-to-end. Ideally we'd be able to eg analyse a single neuron or head in isolation.
    • And hopefully easier to find!
  • They will be composable - rather than needing to understand a full end-to-end circuit, we can understand different modular circuits in isolation, and need only understand the input and output features of each circuit, not the circuits that computed them.
    • Hopefully this also makes it easier to predict model behaviour off distribution, by analysing how interpretable units may compose in unexpected ways!

I think this is just obviously a thing we're going to need to get good at to have a shot at real frontier models! Modular circuits mean that we can both re-use our work from finding circuits before, and hopefully have many fewer levels of composition. But they introduce a new challenge - how do we find exactly what direction corresponds to the feature output by the first circuit, ie the interface between the two circuits? I see two natural ways of doing this:

  • Exploiting a privileged basis - finding interpretable neurons or attention patterns (if this can be thought of as a feature?) and using these as our interpretable foothold.
    • This is great if it works, but superposition means this likely won't be enough.
  • Using probes to find an interpretable foothold in the residual stream or other activations - rather than assuming there's a basis direction, we learn the correct direction
    • This seems the only kind of approach that's robust to superposition, and there's a lot of existing academic work to build upon!
    • But this introduces new challenges - rather than analysing discrete units, it's now crucial to find the right direction and easy to have errors. It seems hard to produce composable circuits if we can't find the right interface.

So what does any of this have to do with Othello-GPT? I think we'll learn a lot by practicing finding modular circuits in Othello-GPT. Othello-GPT has a world model - clear evidence of spontaneous modularity - and our linear probe tells us where it is in the residual stream. And this can be intervened upon - so we know there are downstream circuits that use it. This makes it a great case study! By about layer 4, of the 512 dimensions of the residual stream, we have 64 directions corresponding to which cell has "my colour" and 60 directions corresponding to which cells are blank (the 4 center cells are never blank). This means we can get significant traction on what any circuit is reading or writing from the residual stream.

This is an attempt to get at the "practical knowledge/techniques" part of my breakdown of mech interp bottlenecks - Othello-GPT is a highly imperfect model of LLMs, but I expect finding modular circuits here to be highly tractable and to tell us a lot. Othello-GPT cares a lot about the world model - the input format of a sequence of moves is hard and messy to understand, while "is this move legal" can be answered purely from the board state. So the model will likely devote significant resources to computing board state, forming fairly clean circuits. Yet I still don't fully know how to do it, and I expect it to be hard enough to expose a bunch of the underlying practical and conceptual issues and to teach us useful things about doing this in LLMs.

Gnarly conceptual issues:

  • How to find the right directions with a probe. Ie the correct interface between world-model-computing circuits and world-model-using circuits, such that we can think of the two independently. I see two main issues:
    • Finding all of the right direction - a probe with cosine sim of 0.7 to the "true" direction might work totally fine
      • In particular, can we stop the probe from picking up on features that are constant in this context? Eg "is cell B6 my colour" is only relevant if "is cell B6 blank" is False, so there's naively no reason for the probe to be orthogonal to it.
    • Ignoring features that correlate but are not causally linked - the corner cell can only be non-blank if at least one of the three neighbouring cells are, so the "is corner blank" direction should overlap with these.
      • But my intuition is that the model is learning a causal world model, not correlational - if you want to do complex computations it's useful to explicitly distinguish between "is corner blank" as a thing to compute and use downstream, and all the other features. Rather than picking up on statistical correlations in the data.
  • If we find interpretable directions in the residual stream that are not orthogonal, how do we distinguish between "the model genuinely wants them to overlap" vs "this is just interference from superposition"?
    • Eg, the model should want "is cell A4 blank" to have positive cosine sim with the unembed for the "A4 is legal" logit - non-blank cells are never legal!
  • The world model doesn't seem to be fully computed by layer X and only used in layer X+1 onwards - you sometimes need to intervene before layer 4, and sometimes the calculation hasn't finished before layer 5. How can we deal with overlapping layers? Is there a clean switchover layer per cell that we can calculate separately?
  • How can we distinguish between two features having non-zero dot product because of noise/superposition, vs because they are correlated and the model is using one to compute the other.

Questions I want answered:

  • How can we find the true probe directions, in a robust and principled way? Ideas:
    • Use high weight decay to get rid of irrelevant directions. SGD (maybe with momentum) may be cleaner than AdamW here
    • Use more complex techniques than logistic regression, like amnesiac probing (I found Eleuther's Tuned Lens paper a useful review)
    • Find the directions that work best for causal interventions instead.
    • Maybe use the janky probe directions to try to find the heads and neurons that compute the world model, and use the fact that these are a privileged-ish basis to refine our understanding of the probe directions - if they never contribute to some component of the probe, probably that component shouldn't be there!
    • Maybe implicitly assume that the probe directions should form an orthogonal set
    • Maybe train a probe, then train a second probe on the residual stream component orthogonal to the first probe. Keep going until your accuracy sucks, and then take some kind of weighted average of the residual stream.
  • How is the blank world model computed?
    • This should be really easy - a cell is blank iff it has never been played, so you can just have an attention head that looks at previous moves. Maybe it's done after the layer 0 attention!
    • This is trivial with an attention head per cell, but probably the model wants to be more efficient. What does this look like?
      • Eg it might have a single attention head look at all previous moves with uniform attention. This will get all of the information, but at magnitude 1/current_move, maybe it has the MLP0 layer sharpen this to have constant magnitude?
    • Meta question: What's a principled way to find the "is blank" direction here? The problem is one of converting a three-way classifier (blank vs my vs their) to a binary classifier that can be summarised with a single direction. I'm currently taking blank - (my + their)/2, but this is a janky approach
  • How is the "my vs their" world model computed?
    • This seems like where the actual meat of the problem is!
      • Consider games where
  • Which techniques work well here? My money is on activation patching and direct logit attribution being the main place to start, see activation patching demoed in the accompanying notebook.
    • I'd love for someone to try out attribution patching here!
    • By activation patching, I both mean resample ablations (patching a corrupted activation into a clean run to see which activations are vs aren't necessary) and causal tracing (patching a clean activation into a corrupted run to see which activations contain sufficient information to get the task right)

Preliminary Results On Modular Circuits

The point of this section is to outline exciting directions of future work, but as a proof of concept I've done some preliminary poking around. The meta-level point that makes me excited about this is that linear probes are really nice objects for interpretability. Fundamentally, transformers are made of linear algebra! Every component (layer, head and neuron) reads its input from the residual stream with a linear map, and writes it output by adding it to the residual stream, which is a really nice structure.

Probing across layers: One way this is nice is that we can immediately get a foothold into understanding how the world model is computed. The residual stream is the sum of the embeddings and the output of every previous head and neuron. So when we apply a linear map like our probe, we can also break this down into a direct contribution from each previous head and neuron.

This is the same key idea as direct logit attribution, but now our projection is onto a probe direction rather than the unembed direction for a specific next token. This means we can immediately zoom in to the step of the circuit immediately before the probe, and see which components matter for each cell!

As an example, let's look at move 20 in this game:

The probe can perfectly predict the board state by layer 4

We can now look at how much the output of each attention and each MLP layer contributed to this (concretely we take the output of each attention and each MLP layer on move 30, and project them onto the is_blank direction and the is_mine direction for each cell, and plot this as a heatmap - check the accompanying notebook for details). The MLP layer contributions to whether a cell has my or their colour is particularly interesting - we can see that it normally does nothing, but has a strong effect on the central stripe of cells that were just taken by the opponent - plausibly MLPs calculate when a cell is taken, and attention aggregates this? I'd love to see if there are specific neurons involve.

Reading Off Neuron Weights: Another great thing about a linear probe is that it gives us a meaningful set of directions and subspace in the residual stream (beyond that given by the embedding and unembedding). This means that we can take any component's input or output weights, and project them onto the probe directions to see how that component reads to or writes from the probe's subspace - from this we can often just read off what's going on!

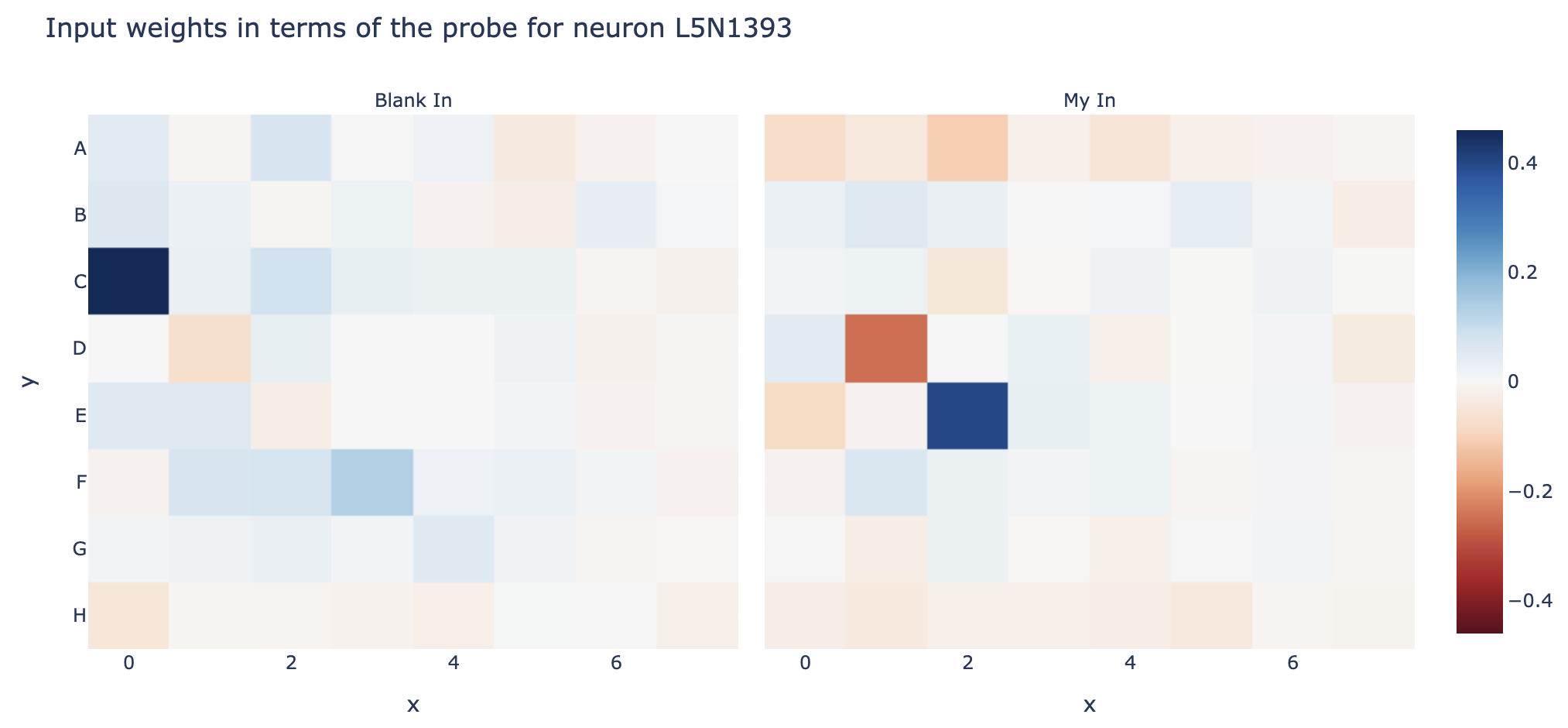
The probe intervention works best between layer 4 and layer 5, so we might hypothesise that some neurons in layer 5 are reading from the probe's subspace - we can check by taking the cosine sim of the neuron's input vector and the probe's directions to see how it responds to each, see the accompanying notebook for details. Here's neuron L5N1393 which seems to mostly represent C0==BLANK & D1==THEIRS & E2==MINE (cherry-picked for reasons unrelated to the probe, discussed more in post 3). Reading the figure: Blue = THEIRS, Red=MINE, White can be either blank or 50-50 mine vs their's, so can't be read easily.

Here's the neurons with the largest standard deviation of activation in layer 3 (a pretty arbitrary way of choosing some that might be interesting) - when we take the cosine sim of the output weights of these and the my colour probe, we see some that are pretty striking (though note that this is only a 0.3 cosine sim, so other stuff may be going on!)

Note that this is a deliberately janky analysis - eg, I'm not ensuring that the probe directions are orthogonal so I may double count, and I'm not looking for other residual stream features. You can track how reasonable this approach by tracking what fraction of the neuron's input is explained by the probe's subspaces, which is 64% in this case (these could otherwise be entirely spurious numbers!).

I go into neuron interpretability in more detail in the next section, but I think this technique is exciting in combination with what I discuss there, because it provides another somewhat uncorrelated technique - if many janky techniques give the same explanation about a neuron, it's probably legit!

Neuron Interpretability and Studying Superposition

As argued earlier, I think that the current biggest open problem in transformer mech interp is understanding the MLP layers of transformers. These represent over 2/3 of the parameters in models, but we've had much more traction understanding attention-focused circuits. I'm not aware of a single public example of what I'd consider a well-understood circuit involving transformer MLP layers (beyond possibly my work on modular addition in a one layer transformer, but that's cheating). There are tantalising hints about the circuits they're used in in eg SoLU and ROME, but I broadly still feel confused re what is mechanistically going on. I think this is a thing we obviously need to make progress on as a field! And I think we'll learn useful things from trying to understand Othello-GPT's MLP layers!

What could progress on understanding MLPs in general look like? I think that we both need to get practice just studying MLP layers, and that we need to form clearer conceptual frameworks. A lot of our intuitions about transformer neurons come from image models, where neurons seem to (mostly?) represent features, have ReLU activations, and seem to be doing fairly discrete kinds of logic, eg "if car wheel present and car body present and car window present (in the right places) -> it's a car".

Transformers are different in a bunch of ways - there's attention layers, there's a residual stream (with significantly smaller dimension than the number of neurons in each layer!), and smoother and weirder GELU activations. Most importantly, polysemanticity seem to be a much bigger deal - single neurons often represent multiple features rather than a feature per neuron - and we think this is because models are using superposition - they represent features as linear combinations of neurons and use this to compress in more features than they have dimensions. This was argued for pretty convincingly in Toy Models of Superposition, but their insights were derived from a toy model, which can easily be misleading. I'm not aware of any work so far exhibiting superposition or properly testing the predictions of that paper in a real model. I expect some ideas will transfer but some will break, and that I'll learn a lot from seeing which is which!

Othello-GPT is far from a real language model, but I expect that understanding its MLP layers would teach me a bunch of things about how transformer MLP layers work in general. The model needs to compress a fairly complex and wide-ranging set of features and computation into just eight layers, and the details of how it does this will hopefully expose some principles about what is and is not natural for a transformer to express in MLP neurons.

What would progress here look like? My high-level take is that a solid strategy is just going out, looking for interesting neurons, and trying to understand them deeply - no grander purpose or high-level questions about the model needed. I'd start with similar goals as I gave in the previous section - look for the neurons that are used to compute the probe, and directly used by the probe. I also outline some further preliminary results that may serve as inspiration.

I've learned a lot from case studies looking deeply at concrete case studies of circuits in models: Interpretability in the Wild found backup heads (that took over when earlier heads were ablated) and negative heads (that systematically boosted incorrect solutions), and the docstring circuit found a polysemantic attention head, and a head which used the causal attention mask to re-derive positional information. I would love to have some similar case studies of meaningful neurons!

Empirically Testing Toy Models of Superposition

The sections of my mech interp explainer on superposition and on the toy models of superposition paper may be useful references

I'm particularly excited about using Othello-GPT to test and validate some of the predictions of Toy Models of Superposition about what we might find in transformers. Empirical data here seems really valuable! Though there are some important ways that the setup of Othello-GPT differs from their toy model. Notably, they study continuous (uniform [0, 1]) features, while Othello-GPT's features seem likely to be binary (on or off), as they're discrete and logical functions of the board state and of the previous moves. Binary features seem more representative of language, especially early token-level features like bigrams and multi-token words, and are also easier to put into superposition, because you don't need to distinguish low values of the correct feature from high values of the incorrect feature

A broader point is whether we expect Othello-GPT to use superposition at all? Their model has more features to represent than dimensions, and so needs to use superposition to pack things in. It's not obvious to me how many features Othello-GPT wants to represent, and how this compares to the number of dimensions - my guess is that it still needs to use superposition, but it's not clear. Some considerations:

  • There's actually a lot of very specific features it might want to learn - eg in the board state -> output logit parts there seems to be a neuron representing C0==BLANK & D1==THEIR'S & E2==MINE, ie can I place a counter in C0 such that it flanks exactly one counter on the diagonal line to the down and right - if this kind of thing is useful, it suggests the model is dealing with a large combinatorial explosion of cases for the many, many similar configurations!
    • Further, computing the board state from the moves also involves a lot of messy cases, eg dealing with the many times and directions a piece can be flipped and combining this all into a coherent story.
      • Reminder: Transformers are not recurrent - it can't compute the board state at move n from the state at move n-1, it needs to compute the state at every move simultaneously with just a few layers of attention to move partial computation forwards. This is actually really hard, and it's not obvious to me how you'd implement this in a transformer!
  • There are two different kinds of superposition, residual stream superposition and neuron superposition (ie having more features than dimensions in the residual stream vs in the MLP hidden layer).
    • The residual stream has 512 dimensions, but there's 8 layers of 2048 neurons each (plus attention heads) - unless many neurons do nothing or are highly redundant, it seems very likely that there's residual stream superposition!
      • Though note that it's plausible it just has way fewer than 2048 features worth computing, and is massively over-parametrised. I'm not sure what to think here!
      • The board state alone consumes 25% of the dimensions, if each feature gets a dedicated dimension, and I expect there's probably a bunch of other features worth computing and keeping around?

Concrete questions I'd want to test here - note that the use of dropout may obfuscate these questions (by incentivising redundancy and backup circuits), and this may be best answered in a model without dropout. These also may be best answered in a smaller model with fewer layers and a narrower residual stream, and so with a stronger incentive for superposition!:

  • Do important features get dedicated dimensions in the residual stream? (ie, orthogonal to all other features)
    • Guesses for important features - whether black or white is playing, the board state, especially features which say which center cells have my colour vs their's.
  • Conversely, can we find evidence that there is overlap between features in the residual stream?
    • This is surprisingly thorny, since you need to distinguish this kind of genuine interference vs intentional overlapping, eg from the source of the first feature actually wanting to contribute a bit to feature two as well.
  • Do the important neurons seem monosemantic?
    • Important could mean many things eg high effect when patching, high average activation or standard deviation of activation, high cost when ablated, or any other range of measurements, high gradient or gradient x activation
    • My workflow would be to use the probe and unembed to interpret neuron weights, max activating dataset examples to help form a hypothesis, and then use a spectrum plot to properly analyse it (discussed more below).
  • Do we get seemingly unrelated features sharing a neuron? The paper predicts superposition is more likely when there are two uncorrelated or anti-correlated features, because then the model doesn't need to track the simultaneous interference of both being there at once.
  • Can we find examples of a feature being computed that needs more than one neuron? Analogous to how eg modular addition uses ReLUs to multiply two numbers together, which takes at least three to do properly. This is a bit of a long shot, since I think any kind of discrete, Boolean operation can probably be done with a single GELU, but I'd love to be proven wrong!
  • Do features actually seem neuron aligned at all?
    • If we find features in superposition, do they tend to still be sparse (eg linear combinations of 5 ish neurons) or diffuse (no noticable alignment with the neuron basis)
  • Can we find any evidence of spontaneous sorting of superposed features into geometric configurations? (A la the toy models paper)
  • Can you construct any adversarial examples using evidence from the observed polysemanticity?
  • Can you find any circuits used to deal with interference superposition? Or any motifs, like the asymmetric inhibition motif?

Preliminary Results On Neuron Interpretability

Note that this section has some overlap with results discussed in my research process

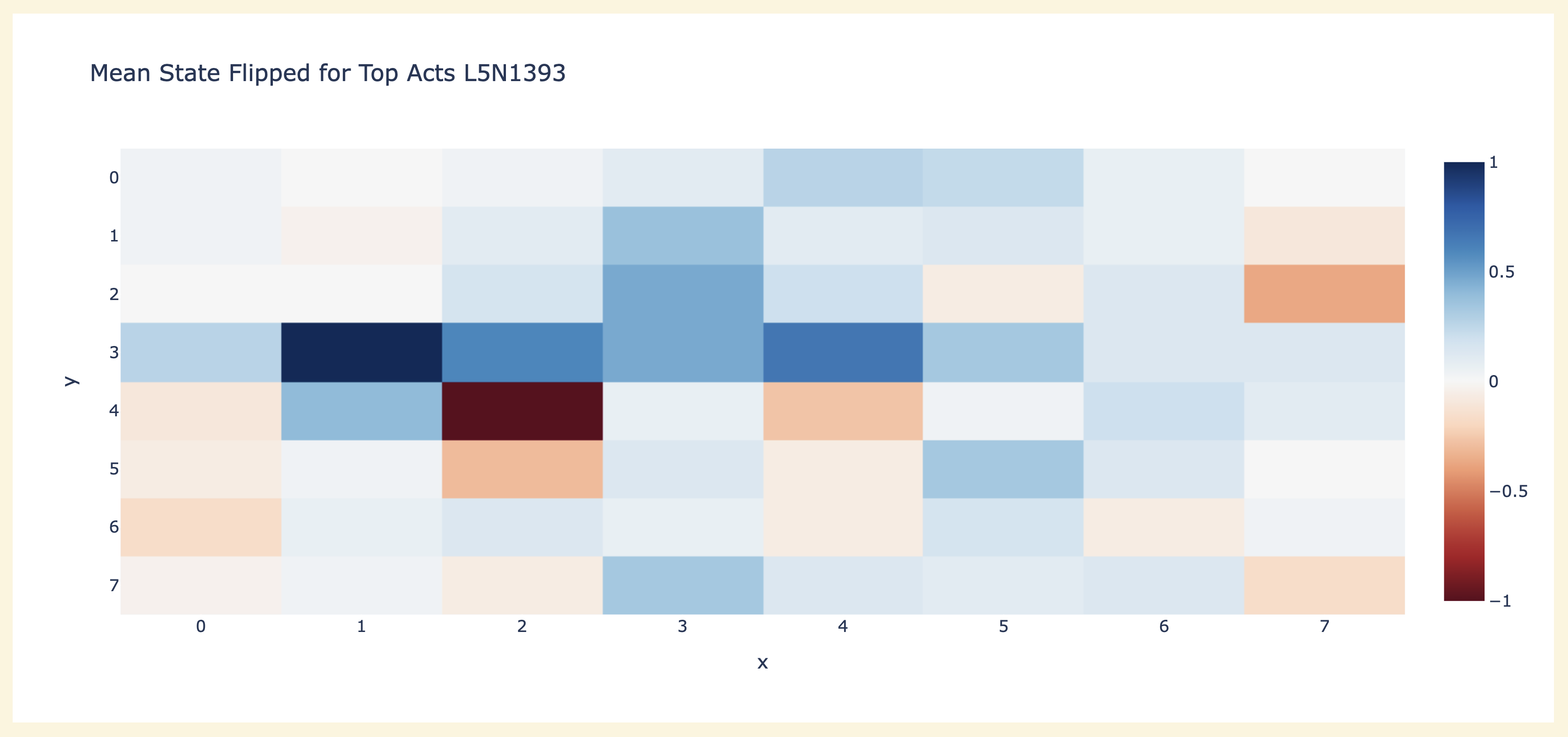
In addition to the results above using the probe to interpret neuron weights, an obvious place to start is max activating dataset examples - run the model over a bunch of games and see what moves the neuron activates the most on. This is actually a fair bit harder to interpret than language, since "what are the connections between these sequences of moves" isn't obvious. I got the most traction from studying board state - in particular, the average number of times each cell is non-empty, and the average number of times a cell is mine vs their's. Here's a plot of the latter for neuron L5N1393 that seems immediately interpretable - D1 is always their's, E2 is always mine! (across 50 games, so 3000 moves) I sometimes get similar results with other layer 5 and layer 6 neurons, though I haven't looked systematically.

Looking at the fraction of the time a cell is blank or not seems to give pretty interesting results for layer 3 and layer 4 neurons.

I expect you can stretch max activating dataset examples further by taking into account more things about the moves - what time in the game they happened, which cells are flipped this turn (and how many times in total!), which cell was played, etc.

My guess from this and probe based analysis earlier was that neuron L5N1393 monosemantically represented the diagonal line configuration C0==BLANK & D1==THEIR'S & E2==MINE. This makes sense as a useful configuration since it says that C0 is a legal move, because it and E2 flank D1! But this seems inconsistent with the direct logit attribution of the neuron (ie the output vector of the neuron projected by the unembed onto the output logits), which seems to boost C0 a lot but also D1 a bit - which seems wildly inconsistent with it firing on D1 being their colour (and thus not a legal place to play!)

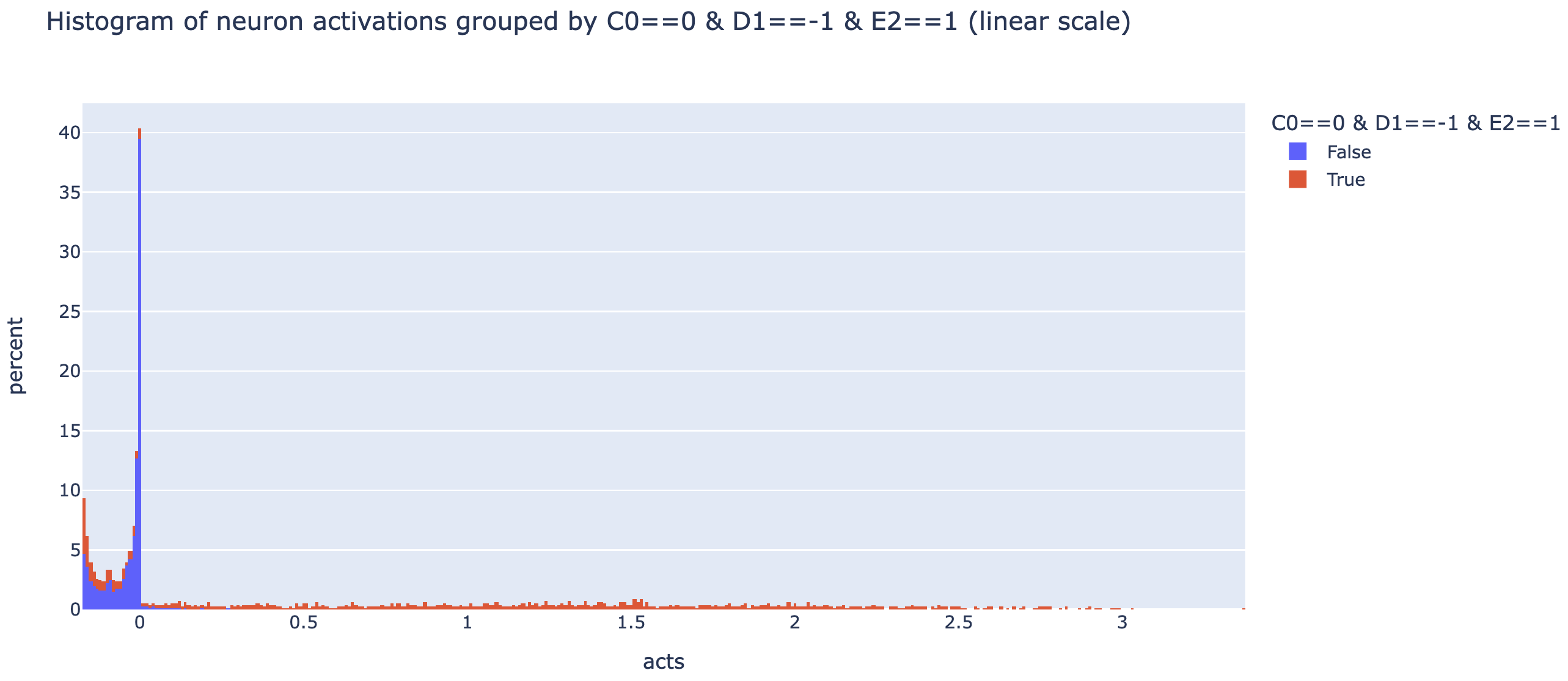
These techniques can all be misleading - max activating dataset examples can cause interpretability illusions, direct logit attribution can fail for neurons that mostly indirectly affect logits, and probes can fail to interpret neurons that mostly read out unrelated features. One of the more robust tools for checking what a neuron means is a spectrum plot - if we think a neuron represents some feature, we plot a histogram of the "full spectrum" of the neuron's activations by just taking the neuron activation on a ton of data, and plotting a histogram grouped by whether the feature is present or not (used in curve detectors and multimodal neurons). If a neuron is monosemantic, this should fairly cleanly separate into True being high and False being low!

Note that the y axis is percent (ie it's normalised by group size so both True and False's histograms add up to 100 in total, though True is far more spread out so it doesn't look it. This is hard to read, so here it is on a log scale (different to read in a different way!).

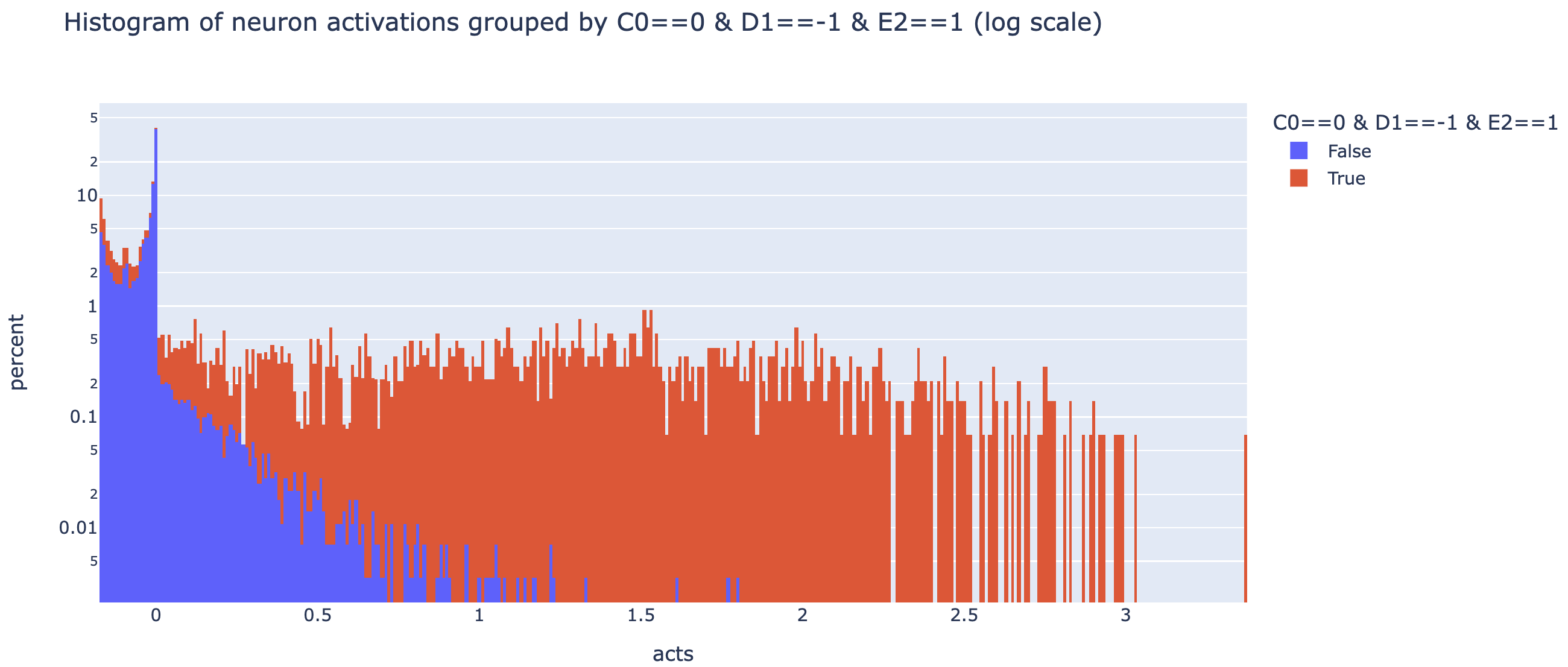
These plots are somewhat hard to interpret, but my impression is that this neuron is plausibly monosemantic-ish, but with a more refined feature - basically all of the high activations have the diagonal line hypothesised, but this is necesssary not sufficient - there's a bunch of negative activations with the line as well! Plausibly it's still monosemantic but there's some extra detail I'm missing, I'm not sure! My next steps would be to refine the hypothesis by inspecting the most positive and most negative True examples, and if I can get a cleaner histogram to then try some causal interventions (eg mean ablating the neuron and seeing if it has the effect my hypothesis would predict). I'd love to see someone finish this analysis, or do a similar deep dive on some other neurons!

Spectrum plots are a pain to make in general, because they require automated feature detectors to do properly (though you can do a janky version by manually inspecting randomly sampled examples, eg a few examples from each decile). One reason I'm excited about neuron interpretability in Othello-GPT is that it's really easy to write automated tests for neurons and thus get spectrum plots, and thus to really investigate monosemanticity! If we want to be able to make real and robust claims to have identified circuits involving neurons or to have mechanistically reverse-engineered a neurons, I want to better understand whether we can claim the neuron is genuinely only used for a single purpose (with noise) or is also used more weakly to represent other features. And a concrete prediction of the toy models framework is that there should be some genuinely monosemantic neurons for the most important features.

That said, showing genuine monosemanticity is hard and spectrum plots are limited. Spectrum plots will still fall down for superposition with very rare features - these can be falsely dismissed as just noise, or just never occur in the games studied! And it's hard to know where to precisely draw the line for "is monosemantic" - it seems unreasonable to say that the smallest True activation must be larger than the largest False one! To me the difference is whether the differences genuinely contribute to the model having low loss, vs on average contributing nothing. I think questions around eg how best to interpret these plots are an example of the kind of practical knowledge I want to get from practicing neuron interpretability!

Case Study: Neurons and Probes are Confusing

As a case study in how this can be confusing, here's an earlier draft graph for the section on finding modular circuits - looking at the output weights of top layer 4 neurons (by std) in the blank probe basis. It initially seems like these are all neurons dedicated to computing that a single cell is blank. And I initially got excited and thought this made a great graph for the post! But on reflection this is weird and surprising (exercise: think through why before you read on)

I argue that this is weird, because figuring out whether a cell is blank should be pretty easy - a cell can never become non-empty, so a cell is blank if and only if it has never been played. This can probably be done in a single attention layer, and the hard part of the world model is computing which cells are mine vs their's. So what's up with this?

It turns out that what's actually going on is that the blank probe is highly correlated with the unembed (the linear map from the final residual to the logits). A cell can be legal only if it is blank, if a cell has a high logit at the end of the model, then it's probably blank. But our probe was computed after layer 6, when there's a lot of extraneous information that probably obscures the blankness information - probably, the probe also learned that if there's going to be a high logit for a cell then that cell is definitely blank, and so the blank directions are partially aligned with the unembed directions. Though on another interpretation, is_blank and the unembed are intentionally aligned, because the model knows there's a causal link and so uses the is_blank subspace to also contribute to the relevant unembed.

And we see that the alignment with the unembed is even higher! (Around cosine sim of 0.8 to 0.9)

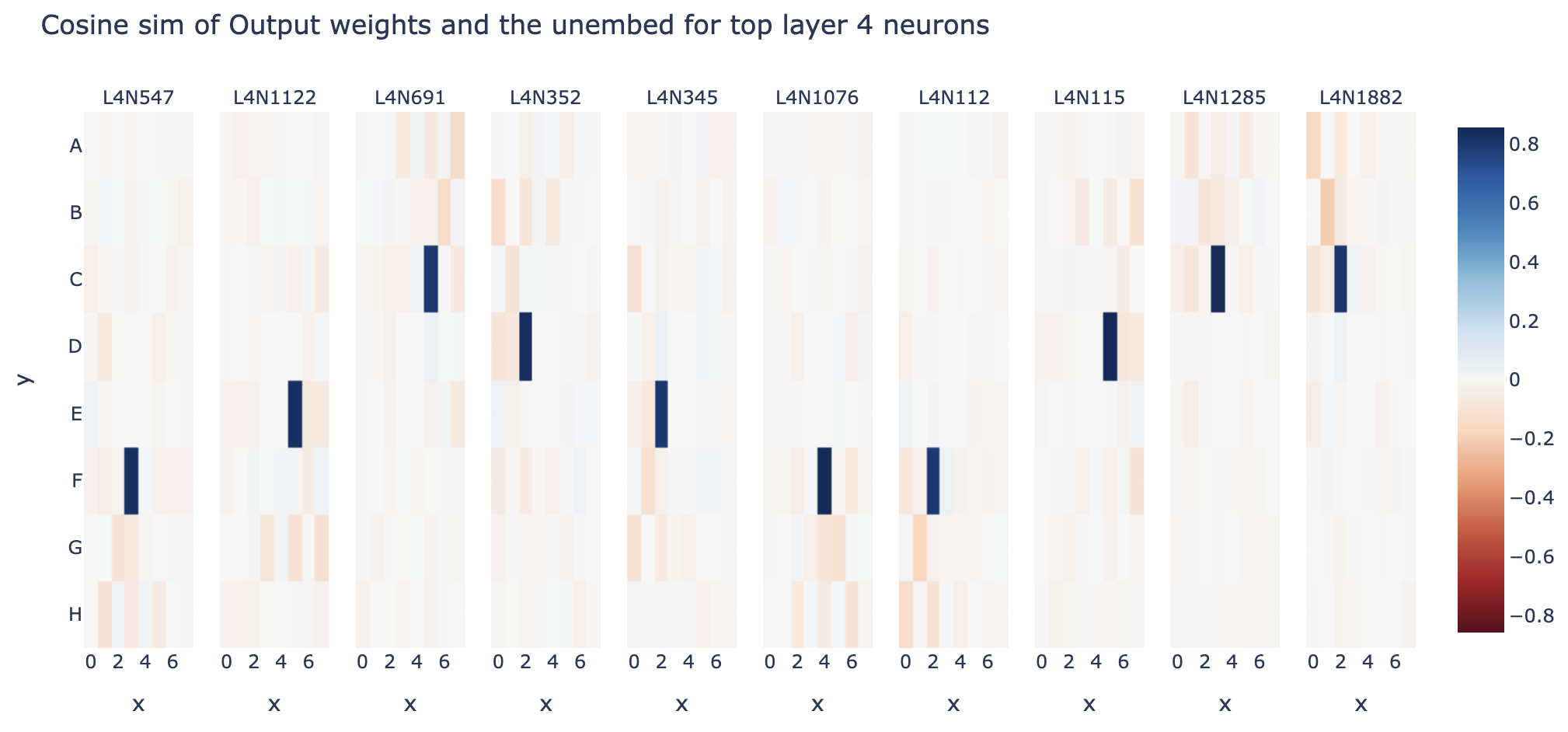
A Transformer Circuit Laboratory

My final category is just the meta level point that I'm confused in many ways about the right conceptual frameworks when thinking about transformer circuits, and think that there's a lot of ways we could make progress here! Just as Othello-GPT helped provide notable evidence for the hypothesis that models form linear representations of features, I hope it can help clarify some of these - by concretely understanding what happens inside of it, we can make more informed guesses about transformers in general. Here's a rough brainstorm of weird hypotheses and confusions about what we might find inside transformers - I expect that sufficient investigation of Othello-GPT will shed light on many of them!

Since Othello-GPT is an imperfect proxy for LLMs, it's worth reflecting on what evidence here looks like. I'm most excited about Othello-GPT providing "existence proofs" for mysterious phenomena like memory management: case studies of specific phenomena, making it seem more likely that they arise in real language models. Proofs that something was not used/needed are great, but need to be comprehensive enough to overcome the null hypothesis of "this was/wasn't there but we didn't look hard enough", which is a high bar!

  • Does it do memory management in the residual stream? Eg overwriting old features when they're no longer needed. I'd start by looking for neurons with high negative cosine sim between their input and output vectors, ie which basically erase some direction.
    • One hypothesis is that it implicitly does memory management by increasing the residual stream norm over time - LayerNorm scales it to have fixed norm, so this suppresses earlier features. If this is true, we might instead observe signal boosting - key features get systematically boosted over time (eg whether we're playing black or white)
    • This might come up with cells that flip many times during previous moves - maybe the model changes its guess for the cell's colour back and forth several times as it computes more flips? Do each of these write to the probe direction and overwrite the previous one, or is it something fancier?
  • Do heads and neurons seem like the right units of analysis of the model? Vs eg entire layers, superposition-y linear combinations of neurons/heads, subsets of heads, etc.
  • Do components (heads and neurons) tend to form tightly integrated circuits where they strongly compose with just a few other components to form a coherent circuit, or tend to be modular, where each component does something coherent in isolation and composes with many other components.
    • For example, an induction head could be either tightly integrated (the previous token head is highly coupled to the induction head and not used by anything else, and just communicates an encoded message about the previous token directly to the induction head) or could form two separate modules, where the previous token head's output writes to a "what was in the previous position" subspace that many heads (including the induction head!) read from
      • My guess is the latter, but I don't think anyone's checked! Most working finding concrete circuits seems to focus on patching style investigations on a narrow distribution, rather than broadly checking behaviour on diverse inputs.
    • On a given input, can we clearly detect which components are composing? Is this sparse?
  • When two components (eg two heads or a head and a neuron) compose with each other, do they tend to write to some shared subspace that many other components read and write from, or is there some specific encod
    • Do components form modules vs integrated circuits vs etc.
  • Can we find examples of head polysemanticity (a head doing different things in different contexts) or head redundancy (multiple heads doing seemingly the same thing).
    • Do we see backup heads? That is, heads that compensate for an earlier head when that head is ablated. This model was trained with attention dropout, so I expect they do!
      • Do these backup heads do anything when not acting as backups?
      • Can we understand mechanistically how the backup behaviour is implemented?
      • Are there backup backup heads?
    • Can we interpret the heads at all? I found this pretty hard, but there must be something legible here!
    • If we find head redundancy, can we distinguish between head superposition (there's a single "effective head" that consists of a linear combination of these )
    • Can we find heads which seem to have an attention pattern doing a single thing, but whose OV circuit is used to convey a bunch of different information, read by different downstream circuits
    • Can we find heads which have very similar attention patterns (ie QK circuits) whose OV circuits add together to simulate a single head with an OV circuit of twice the rank?
  • Is LayerNorm ever used as a meaningful non-linearity (ie, the scale factor differs between tokens in a way that does useful computation), or basically constant? Eg, can you linearly replace it?
    • Are there emergent features in the residual stream? (ie dimensions in the standard basis that are much bigger than the rest). Do these disproportionately affect LayerNorm?
  • The model has clearly learned some redundancy (because it was trained with dropout, but also likely would learn some without any dropout). How is this represented mechanistically?
    • Is it about having backup circuits that takeover when the first thing is ablated? Multiple directions for the same feature? Etc.
  • Can you find more evidence for or against the hypothesis that features are represented linearly?
    • If so, do these get represented orthogonally?
  • Ambitiously, do we have a shot at figuring out everything that the model is doing? Does it seem remotely possible to fully-reverse engineer it?
    • Is there a long tail of fuzzy, half-formed features that aren't clean enough to interpret, but slightly damage loss if ablated? Are there neurons that just do nothing either way?
    • Some ambitious plans for interpretability for alignment involve aiming for enumerative safety, the idea that we might be able to enumerate all features in a model and inspect this for features related to dangerous capabilities or intentions. Seeing whether this is remotely possible for Othello-GPT may be a decent test run.
  • Do the residual stream or internal head vectors have a privileged basis? Both with statistical tests like kurtosis, and in terms of whether you can actually interp directions in the standard basis?
  • Do transformers behave like ensembles of shallow paths? Where each meaningful circuit tends to only involve a few of the 16 sublayers, and makes heavy use of the residual stream (rather than 16 serial steps of computation).
    • Prior circuits work and techniques like the logit lens seems to heavily imply this, but it would be good to get more data!
    • A related hypothesis - when a circuit involves several components (eg a feature is computed by several neurons in tandem) are these always in the same layer? One of my fears is that superposition gives rise to features that are eg linear combinations of 5 neurons, but that these are spread across adjacent layers!

Where to start?

If you've read this far, hopefully I've convinced you there are interesting directions here that could be worth working on! The next natural question is, where to start? Some thoughts:

  • Read the original paper carefully
  • If you're new to mech interp, check out my getting started guide.
    • I particularly recommend getting your head around how a transformer works, and being familiar with linear algebra
  • Use my accompanying notebook as a starting point which demonstrates many of the core techniques
  • My concrete open problems sequence has a bunch of tips on doing good mech interp research, especially in the posts on circuits in toy language models, on neuron interpretability, and on superposition.
  • Read through my notes on my research process to get a sense of what making progress on this kind of work looks like, and in particular the decisions I made and why.

Concrete starter projects

I'll now try to detail some concrete open problems that I think could be good places to start. Note that these are just preliminary suggestions - the above sections outline my underlying philosophy of which questions I'm excited about and a bunch of scattered thoughts about how to make progress on them. If there's a direction you personally feel excited about, you should just jump in.

Ideas for gentle starter projects (Note that I have not actually tried these - I expect them to be easy, but I expect at least one is actually cursed! If you get super stuck, just move on):

  • How does the model decide that the cell for the current move is not blank?
    • What's the natural way for a transformer to implement this? (Hint: Do you need information about previous moves to answer this?)
    • At which layer has the model figured this out?
    • Try patching between two possibilities for the current move (with the same previous game) and look at what's going on
  • Pick a specific cell (eg B3). How does the model compute that it's blank?
    • I'd start by studying the model on a few specific moves. At which layer does the model conclude that it's blank? Does this come from any specific head or neuron?
    • Conceptually, a cell is not blank if and only if it was played as a previous move - how could a transformer detect this? (Hint: A single attention head per cell would work)
  • Take a game where a center cell gets flipped many times. Look at what colour the model thinks that cell is, after each layer and move. What patterns can you see? Can you form any guesses about what's going on? (This is a high-level project - the goal is to form hypotheses, not to reach clear answers)
  • Take the is_my_colour direction for a specific cell (eg D7) and look for neurons whose input weight has high cosine similarity with this. Look at this neuron's cosine sim with every other probe direction, and form a guess about what it's doing (if it's a mess then try another neuron/cell). Example guesses might be
    • Then look at the max activating dataset examples (eg the top 10 over 50 games) and check if your guess worked!
    • Extension: Plot a spectrum plot and check how monosemantic it actually is
  • Repeat the above for the is_blank direction.
  • Take the average of the even minus the average of the odd positional embeddings to get an "I am playing white" direction. Does this seem to get its own dedicated dimension, or is it in superposition?
    • A hard part about answering this question is distinguishing there being non-orthogonal features, vs other components doing memory management and eg systematically signal boosting the "I am playing white" direction so it's a constant fraction of the residual stream. Memory management should act approximately the same between games, while other features won't.

Cleaning Up

This was (deliberately!) a pretty rushed and shallow investigation, and I cut a bunch of corners. There's some basic cleaning up I would do if I wanted to turn this into a real paper or build a larger project, and this might be a good place to start!

  • Training a better probe: I cut a lot of corners in training this probe... Some ideas:
    • Train it on both black and white moves! (to predict my vs their's, so flip the state every other move)
    • I cut out the first and last 5 moves - does this actually help/matter? Check how well the current probe works on early and late moves.
    • The state of different cells will be correlated (eg a corner can only be filled if a neighbouring cell is filled), so the probes may be non-orthogonal for boring reasons. Does it help to constrain them to be orthogonal?
    • What's the right layer to train a probe on?
    • The probe is 3 vectors (three-way logistic regression), but I want a is_blank_vs_filled and is_mine_vs_theirs_conditional_on_not_being_blank direction - what's the most principled way of doing this?
  • Rigorously testing interventions: I'm pretty convinced that intervening the probe does something, but
    • Currently I take the current coordinate with respect to the probe direction, negate that, and then scale. Plausibly, this is dumb and the magnitude of the original coordinate doesn't matter, and I should instead replace it with a constant magnitude. The place I'd start is to just plot a histogram of the coordinates in the probe directions
    • Replicating the paper's analysis of whether their intervention works (their natural and unnatural benchmark)
  • Re-train the model: The model was trained with attention and residual dropout - this is not representative of modern LLMs, and incentivises messy and redundant representations and backup circuits, I expect that training a new model from scratch with no dropout will make your life much easier. (Note that someone is currently working on this)
    • The current model is 8 layers with a residual stream of width 512. I speculate this is actually much bigger than it needs to be, and things might be cleaner with fewer layers and a wider stream, a narrower stream, or both.

The Research Process

This project was a personal experiment in speed-running doing research, and I got the core results in in ~2.5 days/20 hours. This post has some meta level takeaways from this on doing mech interp research fast and well, followed by a (somewhat stylised) narrative of what I actually did in this project and why - you can see the file tl_initial_exploration.py in the paper repo for the code that I wrote as I went (using VSCode's interactive Jupyter mode).

I wish more work illustrated the actual research process rather than just a final product, so I'm trying to do that here. This is approximately just me converting my research notes to prose, see the section on process-level takeaways for a more condensed summary of my high-level takeaways.

The meta level process behind everything below is to repeatedly be confused, plot stuff a bunch, be slightly less confused, and iterate. As a result, there's a lot of pictures!

Takeaways on doing mech interp research

Warning: I have no idea if following my advice about doing research fast is actually a good idea, especially if you're starting out in the field! It's much easier to be fast and laissez faire when you have experience and an intuition for what's crucial and what's not, and it's easy to shoot yourself in the foot. And when you skimp on rigour, you want to make sure you go back and check! Though in this case, I got strong enough results with the probe that I was fairly confident I hadn't entirely built a tower of lies. And generally, beware of generalising from one example - in hindsight I think I got pretty lucky on how fruitful this project was!

  • Be decisive: Subjectively, by far the most important change was suppressing my perfectionism and trying to be bold and decisive - make wild guesses and act on them, be willing to be less rigorous, etc.
    • If I noticed myself stuck on doing the best or most principled thing, I'd instead try to just do something.
      • Eg I wanted to begin by patching between two similar sequences of moves - I couldn't think of a principled way to change a move without totally changing the downstream game, so I just did the dumb thing of patching by changing the final move.
      • Eg when I wanted to try intervening with the probe, I couldn't think of a principled way to intervene on a bunch of games or to systematically test that this worked, or exactly how best to intervene, so I decided to instead say "YOLO, let's try intervening in the dumbest possible way, by flipping the coefficient at a middle layer, on a single move, and see what happens"
    • Pursue the hypothesis that seems "big if true"
      • Eg I decided to try training a linear probe on just black moves after a hunch that this might work given some suggestive evidence from interpreting neuron L5N1393
    • Notice when I get stuck in a rabbit hole/stop learning things and move on
      • Eg after training a probe I found it easy to be drawn into eg inspecting more and more neurons, or looking at head attention patterns, and it worked much better to just say
    • Be willing to make quick and dirty hacks
      • Eg when I wanted to look at the max activating dataset examples for neurons, I initially thought I'd want to run the model on thousands to millions of games, to get a real sample size. But in practice, just running the model on a batch of 100 games and taking the top 1% of moves by neuron act in there, worked totally fine.
  • The virtue of narrowness - depth over breadth: A common mistake in people new to mech interp is to be reluctant to do projects that feel "too small" - eg interpreting a single neuron or head rigorously. And to think that something is interesting only if it's automatable and scalable. But here, being willing to just dive in to patching on specific examples, targeting specific neurons that stood out, etc worked great, and ultimately pointed me to the general principles underlying the model (namely, that it thought in mine vs their's)
  • Gain surface area: I felt kinda stuck when figuring out where to start. Early on, by far the most useful goal was to gain surface area on the problem - to just dive into anything that seemed interesting, play around, and build intuitions about the moving parts of the model and how it was behaving, without necessarily having a concrete goal beyond understanding and following my curiosity.
    • A good way of doing this was to play around with concrete examples, and in particular to patch between similar examples and analyse where the differences came from.
  • Work on algorithmic problems: Empirically, algorithmic problems are just way cleaner and more tractable to interpret - there's a ground truth, it's easier to reason about, and it's easy to craft synthetic inputs. This is a double-edged sword, since they're also less interesting and less true to real models, but it's very convenient for goodharting on "research insight per unit hour"
  • Domain knowledge is super useful!
    • Spending 30-60 minutes at the start playing against the eOthello AI was really valuable for building intuitions (I went in knowing absolutely nothing about Othello), though I got carried away by how fun it was and could have got away with less time.
      • Eg that the start and end of the game are weird, that you occasionally need to pass but can basically ignore it, that a single piece can change colour many times, including from a move pretty far away, and even dumb things like "you can take diagonally, and this happens a lot"
    • Having experience doing mech interp helped a ton - being better able to generate hypotheses, figure out what's interesting, reach for the right techniques, and interpret results
      • In particular, having stared at the mechanical structure of a transformer and what kinds of algorithms are and are not natural to implement remains super useful for building intuitions. (I try to convey a bunch of these in my walkthrough of A Mathematical Framework)
  • Good tooling is crucial: If you want to do research fast, tight feedback loops are key, and having good, responsive tooling that you understand well is invaluable, even for a throwaway project on a tight deadline. I've created an accompanying colab with most of my tools, and I hope they're useful! (Sorry for the jankiness)
    • TransformerLens is a library I made for mech interp of language models, with the explicit goal of making exploratory research easier, and it worked great here! Eg for easily caching model activations, and for trying out different patching and interventional experiments.
      • In general, it's far easier to use software you've written yourself, but I've heard good things from other people trying to use TransformerLens!
    • Building good visualisations was pretty valuable - especially visualising model logits as a heatmap on the board, and converting a set of moves into a plot of the state of the board. Though I probably spent ~4 hours on making beautiful plotly visualisations (and debugging plotly animations...), and could have gotten away with much less.
    • Basic software engineering - noticing the code I kept writing and converting it to functions (eg dumb stuff around changing moves from nice written notation, to the model's vocabulary, to the format used to compute board state; or intervening with the probe; or converting a set of moves to a list of valid moves at each turn, etc)
  • MLPs > attention: I went into this expecting it to be way easier to interpret attention heads/patterns, but I actually didn't make much headway there, but did great with MLP neurons.
    • I think the difference was that I didn't really know how to think about the sequence of prior moves (and thus which moves were attended to), while I did know how to think about the current board state and thus about valid output logits (and direct logit attribution) and about the max activating dataset examples).
    • And the fact that there were seemingly a bunch of monosemantic neurons, rather than a polysemantic mess of superposition
  • Activation patching is great: Models are complex and full of many circuits for different tasks - even on a single input, likely many circuits are relevant to completing the task! This makes it difficult to isolate out anything specific, and thus is hard to be concrete. Activation patching/causal tracing is a great way to get around this - you set up two similar inputs that differ in one crucial detail, and you patch specific activations between the two and analyse what changes (eg whether an output logit changes). Because the two inputs are so similar, this controls for all the stuff you don't care about, and lets you isolate out a specific circuit.

Getting Started

There was first a bunch of general figuring stuff out and getting oriented - learning how Othello worked, reading the existing code, loading in the data and games, figuring out how to convert a sequence of moves into a board state and valid moves, getting everything into a format I could work easily with (eg massive tensors of game moves rather than a list of lists) and making pretty plotting functions. I also decided to filter out weird edge cases I didn't really care about, like games of less than 60 moves, or with passes in them. In hindsight, it would have been better to do some of this later when I had a clearer picture of what did and did not need optimisation, but *shrug*.

The most useful bits of infrastructure I set up (both now, and later) were:

  • Convenience functions to convert moves between 1 to 60 (inputs and outputs of the model, since center squares can't be player), 0 to 63 as the actual indexes, and A0 to H7 as the printable labels
  • Plotting function to plot either a single board state (and valid moves), and an animation showing a whole game with a slider (the latter turned out to be a deep rabbit hole of Plotly animation bugs though...)
  • Creating a single tensor of all games stacked together (in my case, I took all 4.5M games, since it fit into my RAM - 10,000 would have been more than enough)
  • Running and caching the model activations on 100 games, so I could use this as an easy reference without needing to run the model every time (eg to look at neurons with big average activations)

I didn't have a clear next step (my main actual idea was taking one of the author's pre-trained non-linear probes and trying to interpret how that worked, but this seemed like a pain), so I tried to start gaining surface area on what was going on by just trying shit. It's easy to interpret the output logits, and so looking at how each model component directly affects the logits is a good hook to get some insight in any model.

The first actual research I tried was inputting an arbitrary game, and looking at the direct logit attribution of each layer's output on a few of the moves. Eyeballing things, there was a clearish trend where MLP5, MLP6 and Attn7 mattered a lot, other parts were less important. Interestingly, MLP7 (naively, the obvious place to start, since it can only affect the output logits). Example graph below:

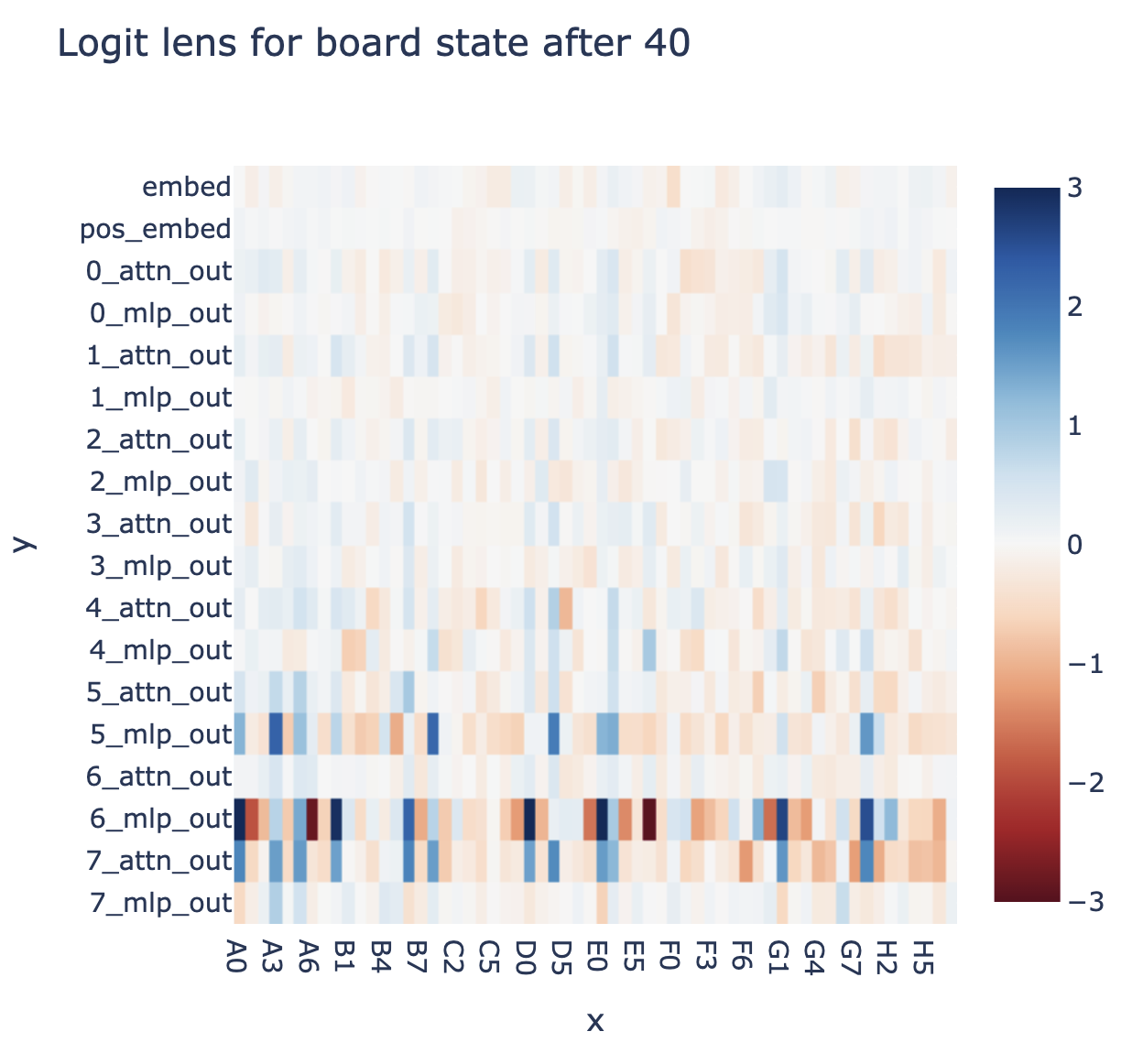
Being more systematic supported this. This is a bit of a weird problem, because there are many (and a variable number of!) valid next moves, rather than a single correct next token, so I tried to both look at the difference in average direct logit attribution for the correct/incorrect next logit, and the difference in min/max contribution. The former doesn't capture bits that disambiguate between borderline correct and borderline incorrect moves, since most moves will be obviously bad, and the latter is misleading because you're taking the max and min over large-ish sets, which is always sketchy (eg it gives misleading results for random noise) - you get a weird spectrum from early to late moves because there are more options in the middle. I also saw that layer 7 acts very differently at the first and last move, presumably because those are easier special cases, but decided this was out of scope and to ignore it for now. I tried breaking the attention layers down into separate heads, but didn't have much luck.

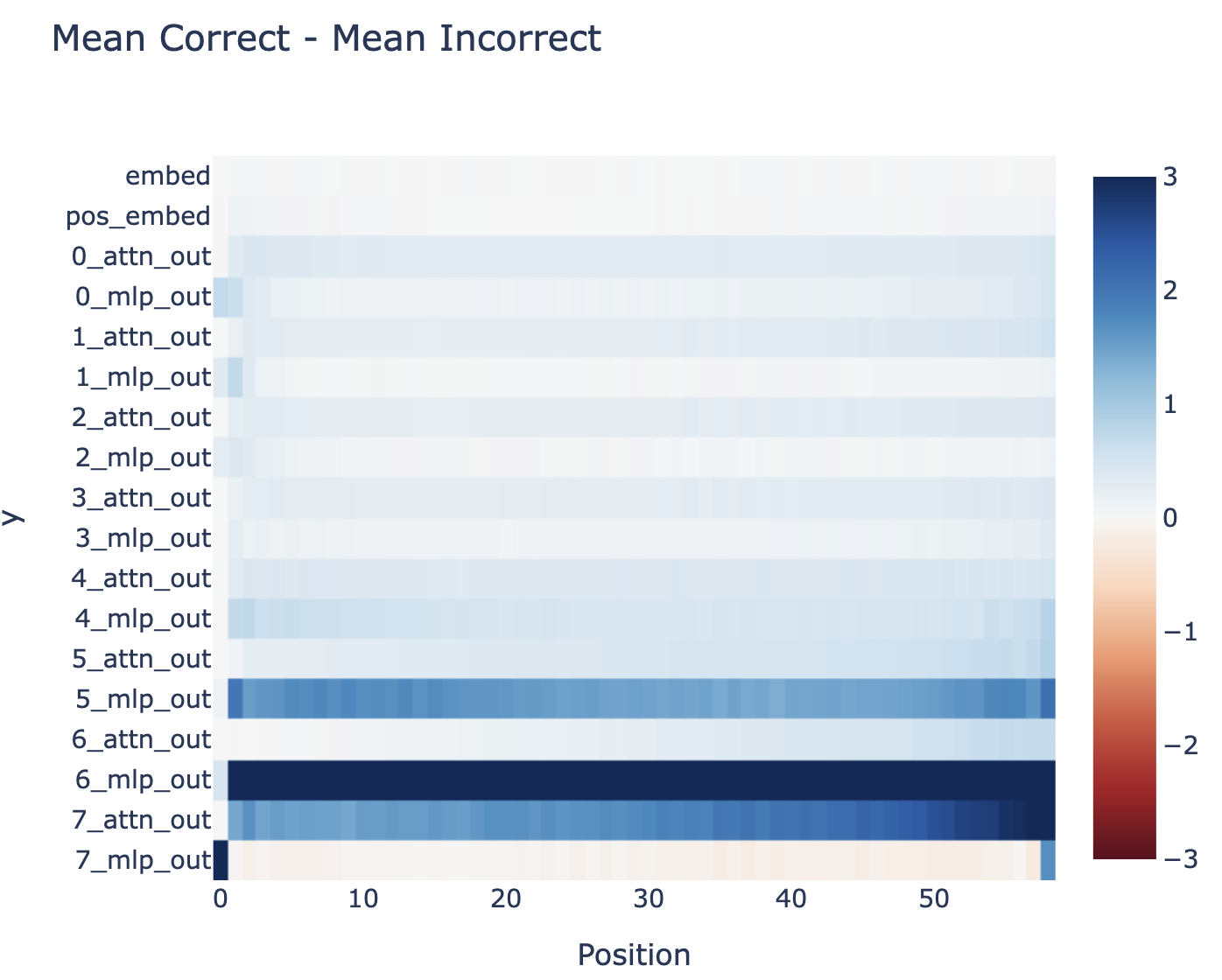
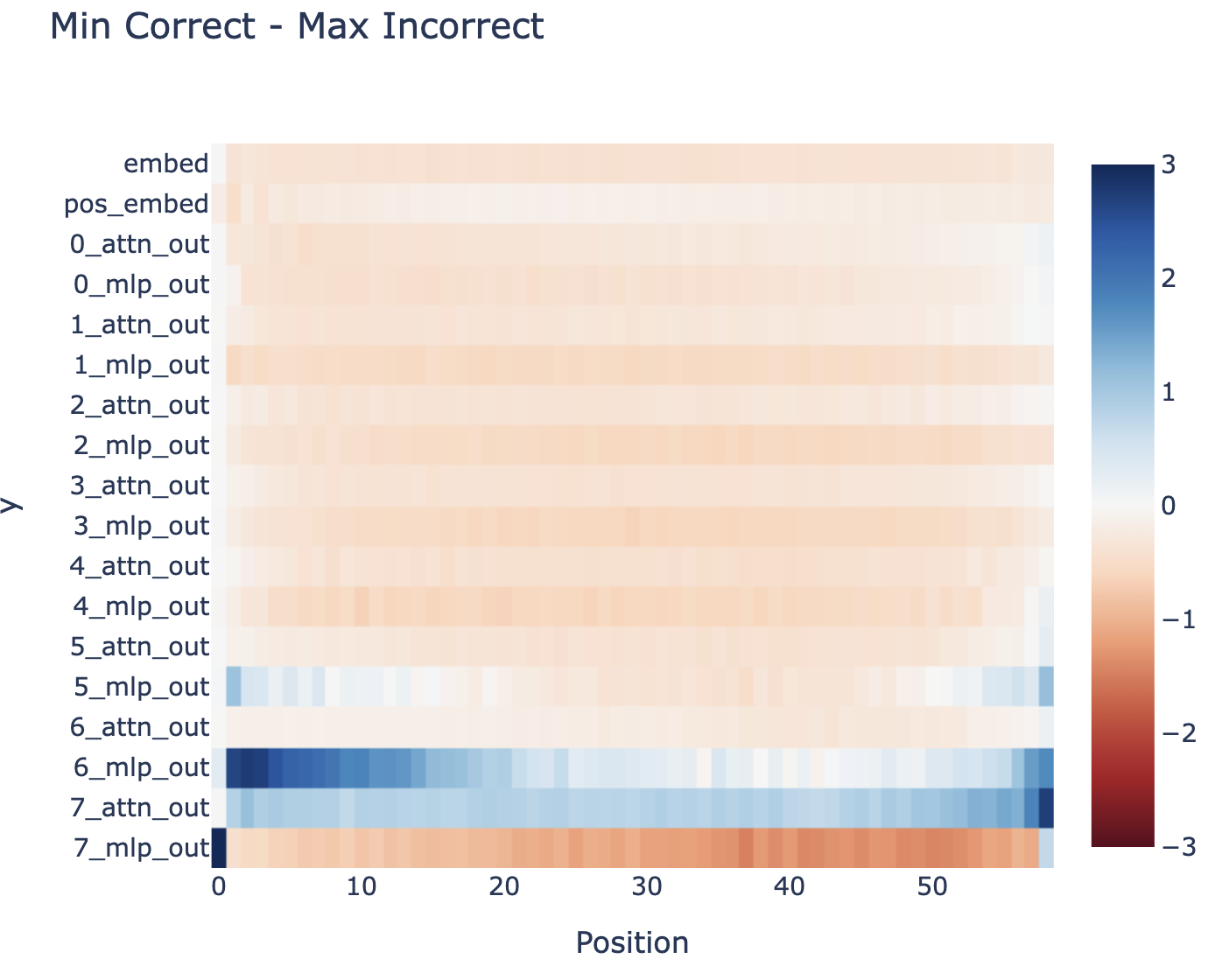
I was then kinda stuck. I tried plotting attention patterns and staring at them, looking for interesting heads, and didn't get much traction (in part because I didn't really get how to interpret moves!). I did see some heads which only attended to moves of the same parity as the current one, which was my first hint for what was going on (not that I noticed lol).

Patching

Part of why interpreting models is hard is because they're full of different circuits that combine to answer a question. But each circuit will only activate on certain inputs, and each input will likely require a bunch of circuits, making it a confusing mess.

Activation patching is a great way to cut through this! The key idea is to set up a careful counterfactual, where you have two inputs, a clean input and a corrupted input, which differ in one key detail. Ideally, the difference between any activation on the clean and corrupted run will purely represent that key detail. You can then iterate over each activation and patch them from the clean run to the corrupted run to see which can most recover the clean output (or from the corrupted run to the clean run to see which can most damage the clean output), and hopefully, a few activations matter a lot and most don't. This can let you isolate which activations actually matter for this detail!

I knew that I wanted to try patching something, but sadly it was kind of a mess, because an input needs to be a sequence of legal moves. I wanted two sequences which had similar board states but whose moves differed in some key places, so I could track down how board state was computed.

I gave up on this idea because it seemed too hard, and instead decided to be decisive and do the dumb thing of changing just the most recent move! I picked an arbitrary game, took the first 30 moves, and changed the final move from H0 to G0 to get a corrupted input. This changed cell C0 (I index my columns at zero not one, sorry) from legal to illegal. This meant I could take the C0 logit as my patching metric - it's high on clean, low on corrupted, and so it can tell me how much my patched activation tracks "the way that the most recent move being G0 rather than H0 is used to determine that C0 is illegal" (or vice versa). This is a very niche thing to study, but it's a start! And the virtue of narrowness says to favour deep understanding of something specific, over aiming for a broad understanding but not knowing where to start.

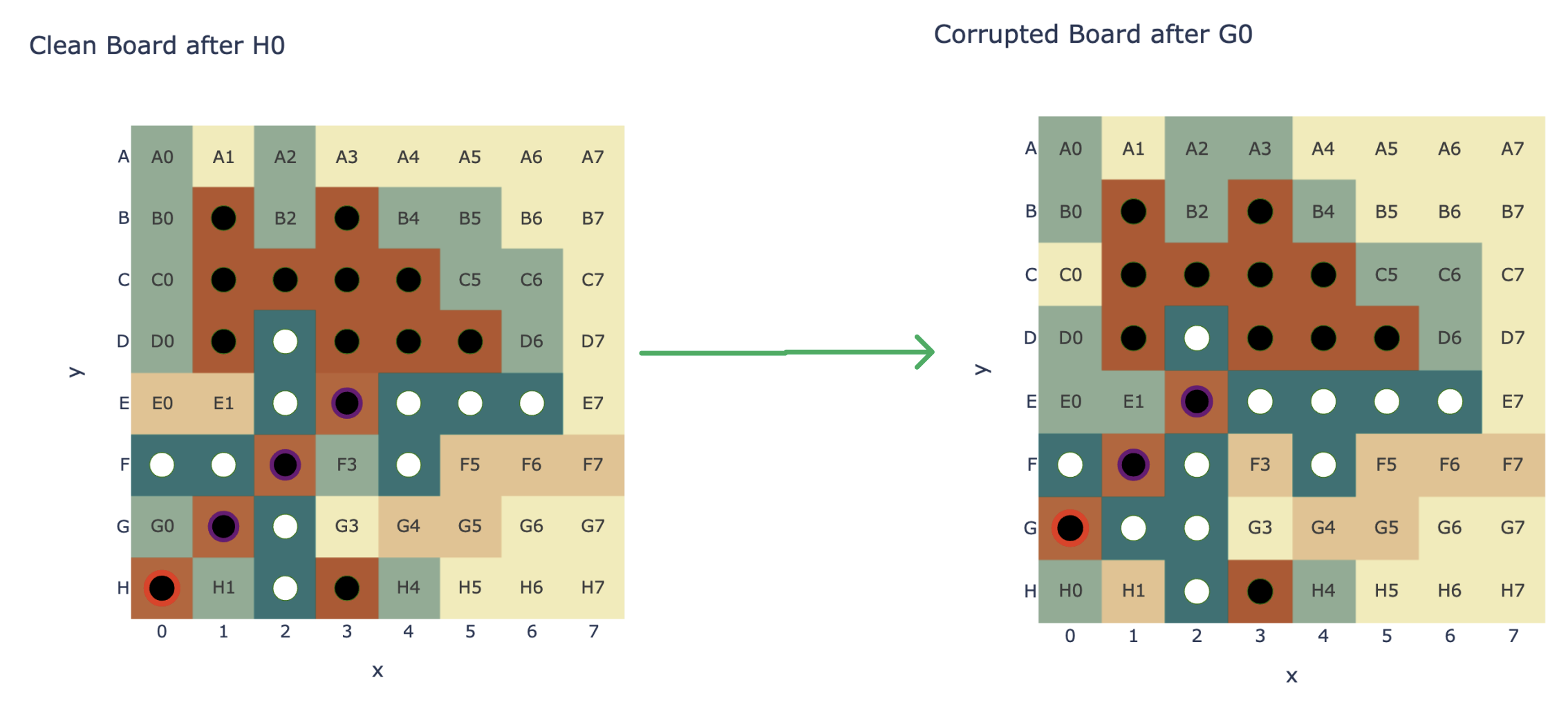
The first thing to try is patching each layer's output - I found that MLP5, MLP6 and MLP0 mattered a lot, Attn7 and MLP4 mattered a bit. The rest didn't matter at all, so I could probably ignore them!

I now wanted to narrow things down further, and got a bit stuck again - I needed to refine "this layer matters" into something more specific. I had the prior that it's way easier to understand attention than MLPs, so I tried looking at the difference in attention pattern from clean to corrupted for each head (from each source token to the final move), but I couldn't immediately see anything interesting (though in hindsight, I see alternating bands of on and off!):

I then just tried looking at the difference in direct logit attribution (to C0) between clean and corrupted for every neuron. This looked way more promising - most neurons were irrelevant, but a few mattered a ton. This suggested I could mostly ignore everything except the neurons that mattered. This gave me, like, 10 neurons to understand, which was massive progress! Bizarrely, MLP7 had two neurons, which both mattered a ton, but near exactly cancelled out (+2.43 v -2.47).

Tangent on Analysing Neurons

Finding that there were clean and interpretable neurons was exciting, and I got pretty side tracked looking at neurons in general - no particular goal, just trying to gain surface area and figure out what was up. Looking at the neuron means across 100 games on the middle moves ([5:-5]) showed that there were some major outliers, and that layer 6 and 7 were the biggest by far. (The graph is sorted, because it's really hard to read graphs with 2000 points on the x axis with no meaningful ordering!)

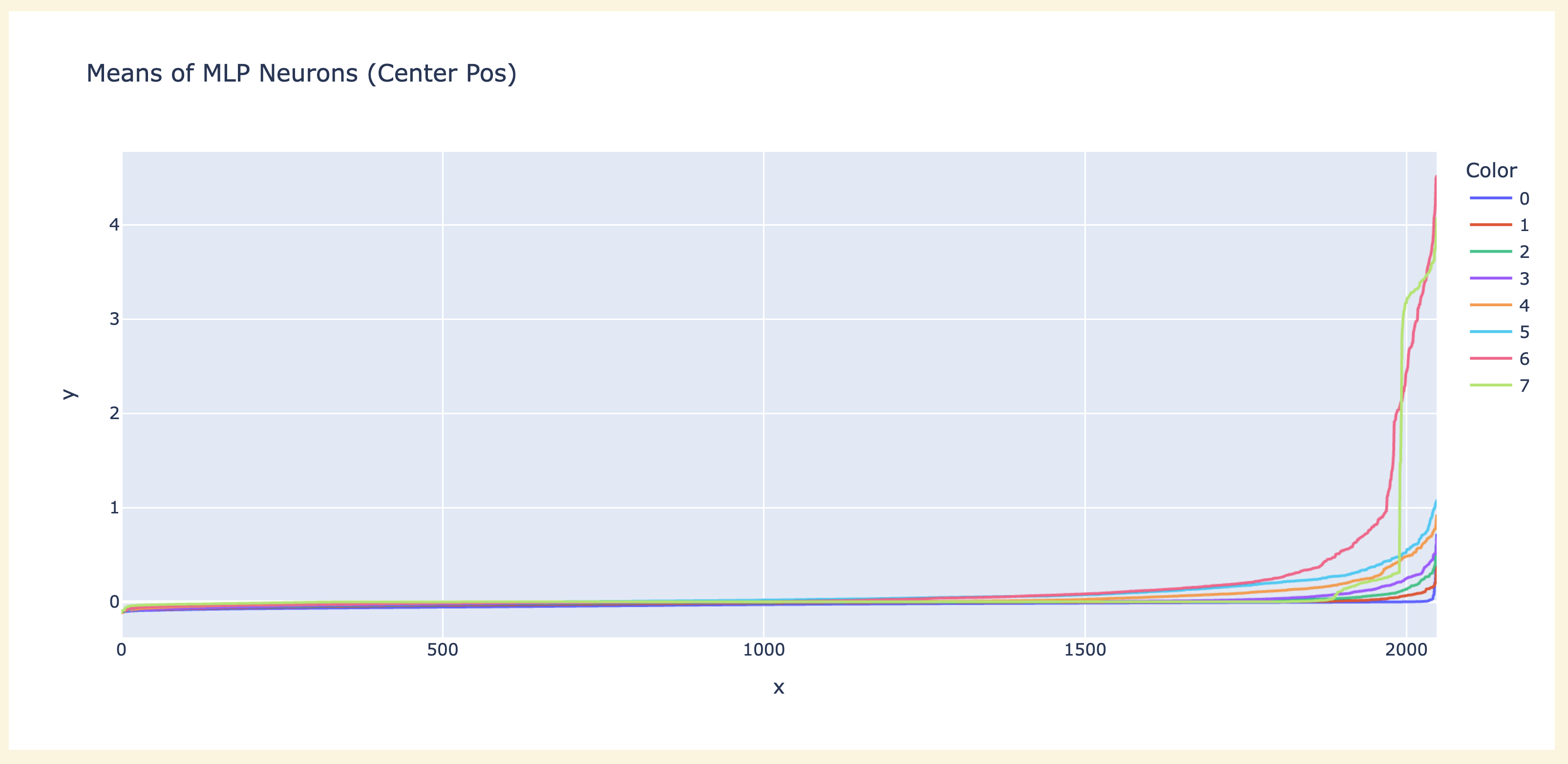
I then tried looking at the direct logit attribution of the top neurons in each layer (top = mean > 0.2, chosen pretty arbitrarily), and they seemed super interpretable - it was visually extremely sparse, and it looked like many neurons connected to a single output logit. Layer 7 had some weird neurons that seemed specialised to the first move. Aside: I highly recommend plotting heatmaps like this with 0 as white - makes it much easier to read positive and negative things visually (this is the plotly color scheme RdBu, px.imshow(tensor, color_continuous_scale='RdBu', color_continuous_midpoint=0.0) works to get these graphs)

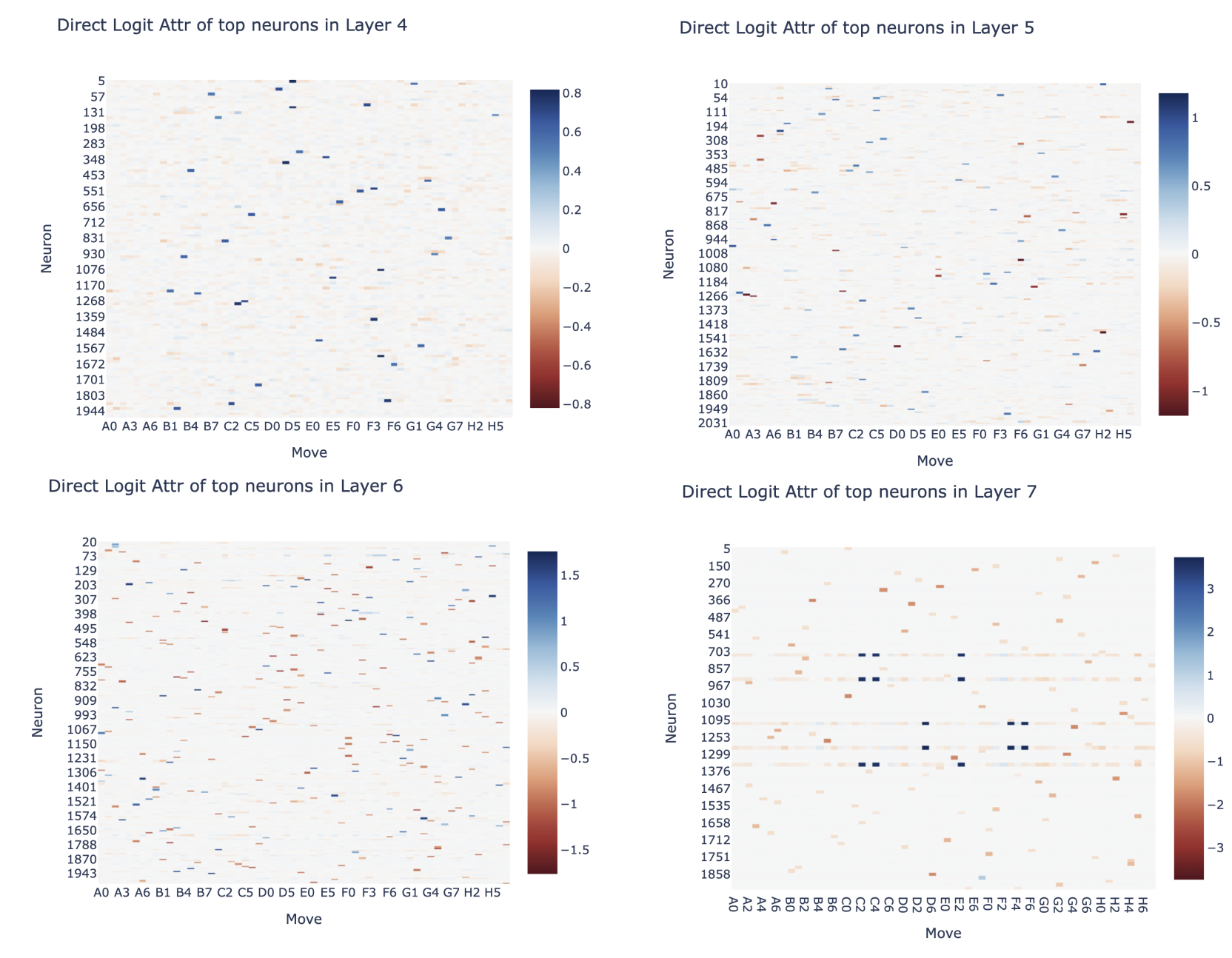
Back to patching

I then ran out of steam and went back to patching. I now tried to patch in individual heads and look at their effect on the C0 logit (now normalised such that 1 means "fully recovered" and 0 means "no change"). Head L7H0 was the main significant one, but I couldn't get much out of it.

I then tried patching in individual neurons - doing all 16000 would be too slow, so I just took the neurons with highest activation difference and patched in those - activation difference had some big outliers. I first tried resample ablating (replacing a clean neuron with corrupted and seeing what breaks) and found that none were necessary (this isn't super surprising - neurons are small, and dropout incentivises redundancy), though the layer 7 neurons matter a bit (they directly affect the logits, so this makes sense!)

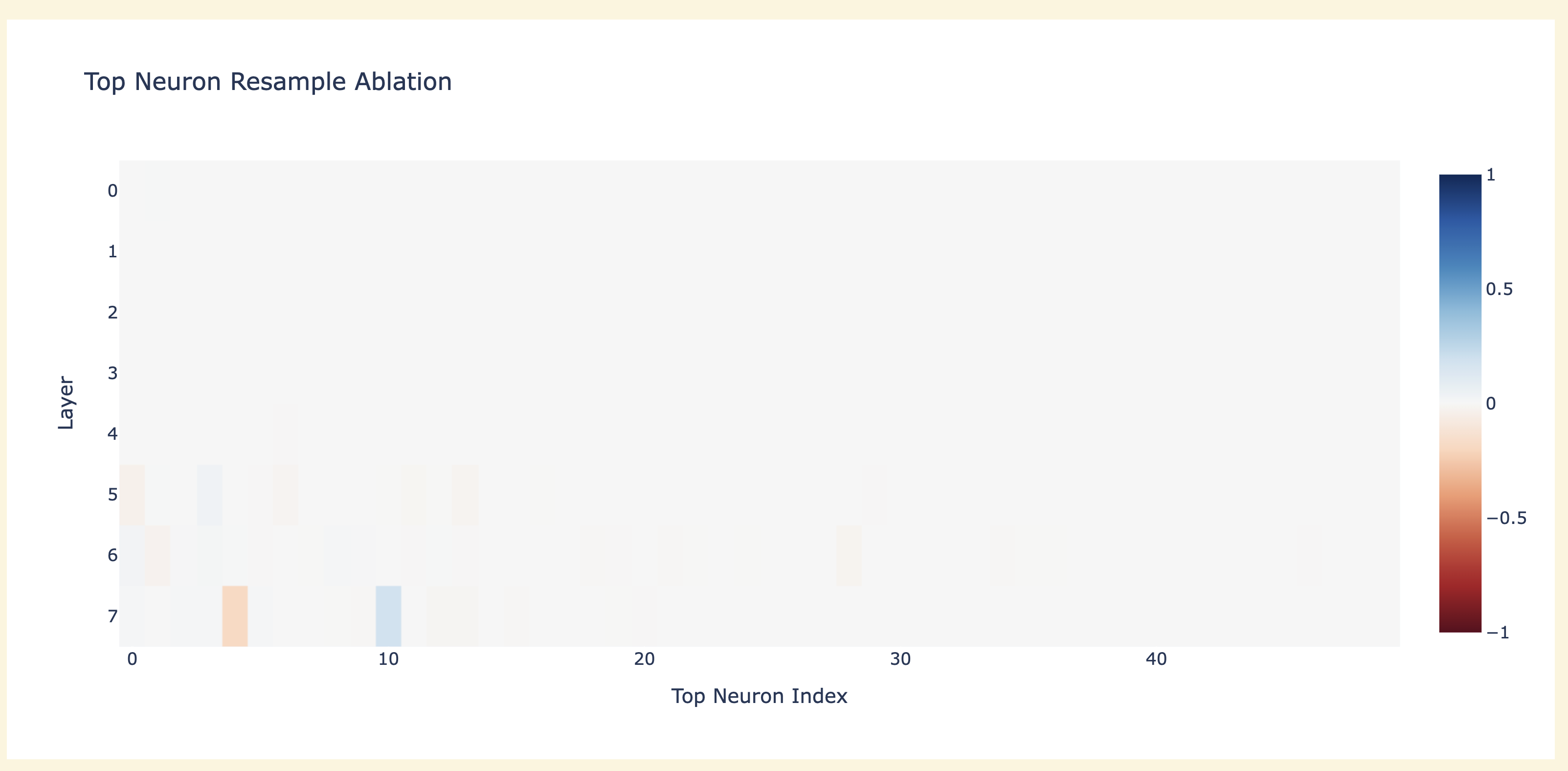
But when I tried causal tracing (replacing a corrupted neuron with its clean copy) I got some striking results - several neurons mattered a bunch, and L5N1393 was enough to recover 75% on its own?! (Notably, this was a significantly bigger effect than just its direct logit attribution)

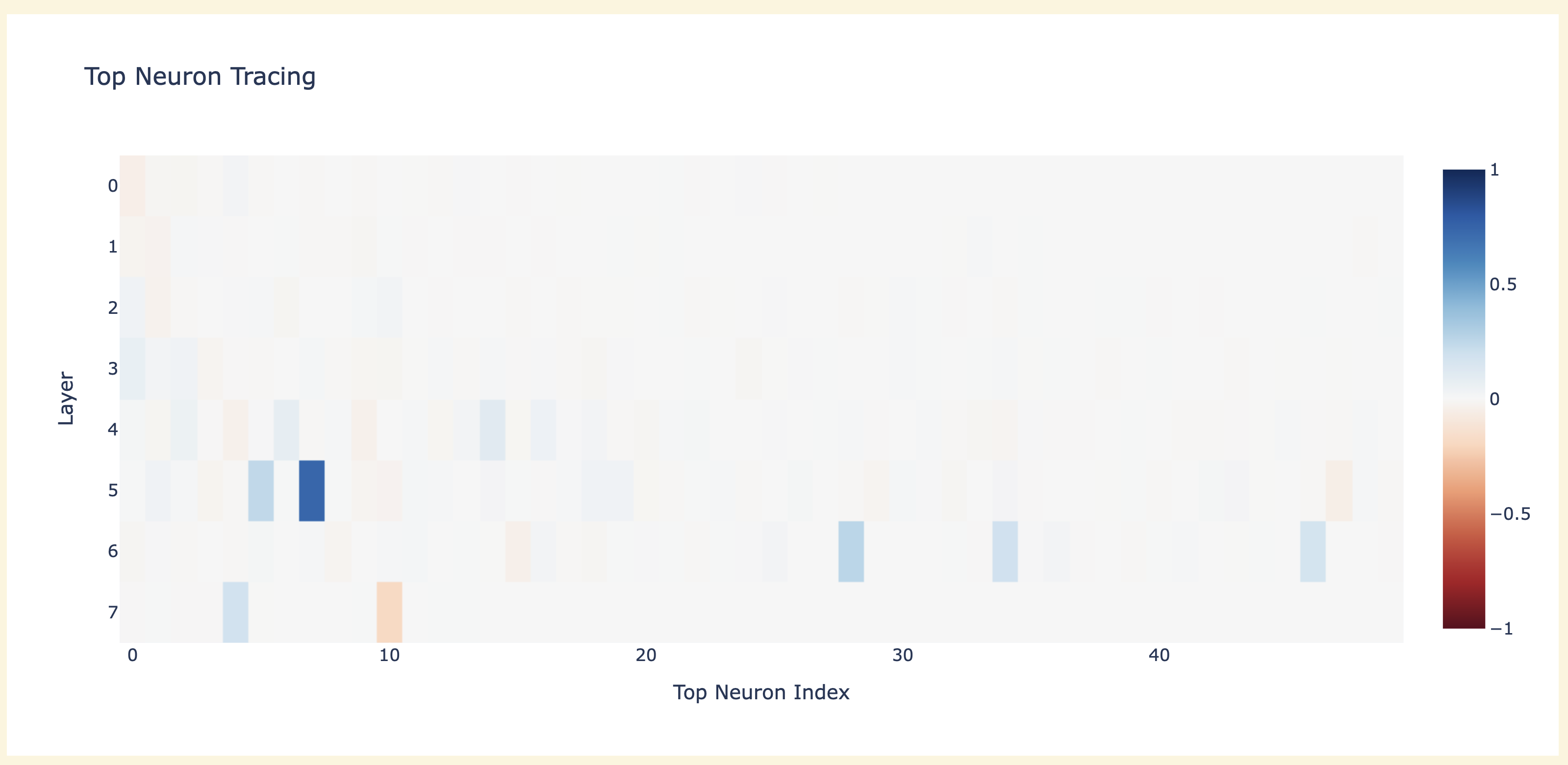
Neuron L5N1393

This was a sufficiently wild result that I pivoted to focusing on that neuron (the 1393th in layer 5).

My starting goal was the incredibly narrow question "figure out why patching in just that neuron into the corrupted run is such a big deal". Again, focus on understanding a narrow questions deeply and properly, even against a flinch of "this is too narrow and there's no way it'll generalise!".

To start with, I cached all activations on the run with a corrupted input but a clean neuron L5N1393, and started comparing the three. The obvious place to start was direct logit attribution of layers - MLP7 went from not mattering in either clean or corrupted to being significant?!

Digging into the MLP7 neurons and their direct logit attribution, I found that both clean and corrupted had a single, dominant, extremely negative neuron. But in the patched run, both were significantly suppressed. My guess was that this was some dropout solving circuit firing, and thus that MLP7 was mostly to deal with dropout - I subjectively decided this didn't seem that interesting and moved on. Interestingly, this is similar to how negative name movers in the Indirect Object Identification circuit act as backups - they significantly suppress the model's ability to do the task, but if you ablate the positive name movers they'll significantly reduce their negative effect to help compensate. (There it's likely a response to attention dropout)

It also significantly changed some layer 6 neurons, which seemed maybe more legit:

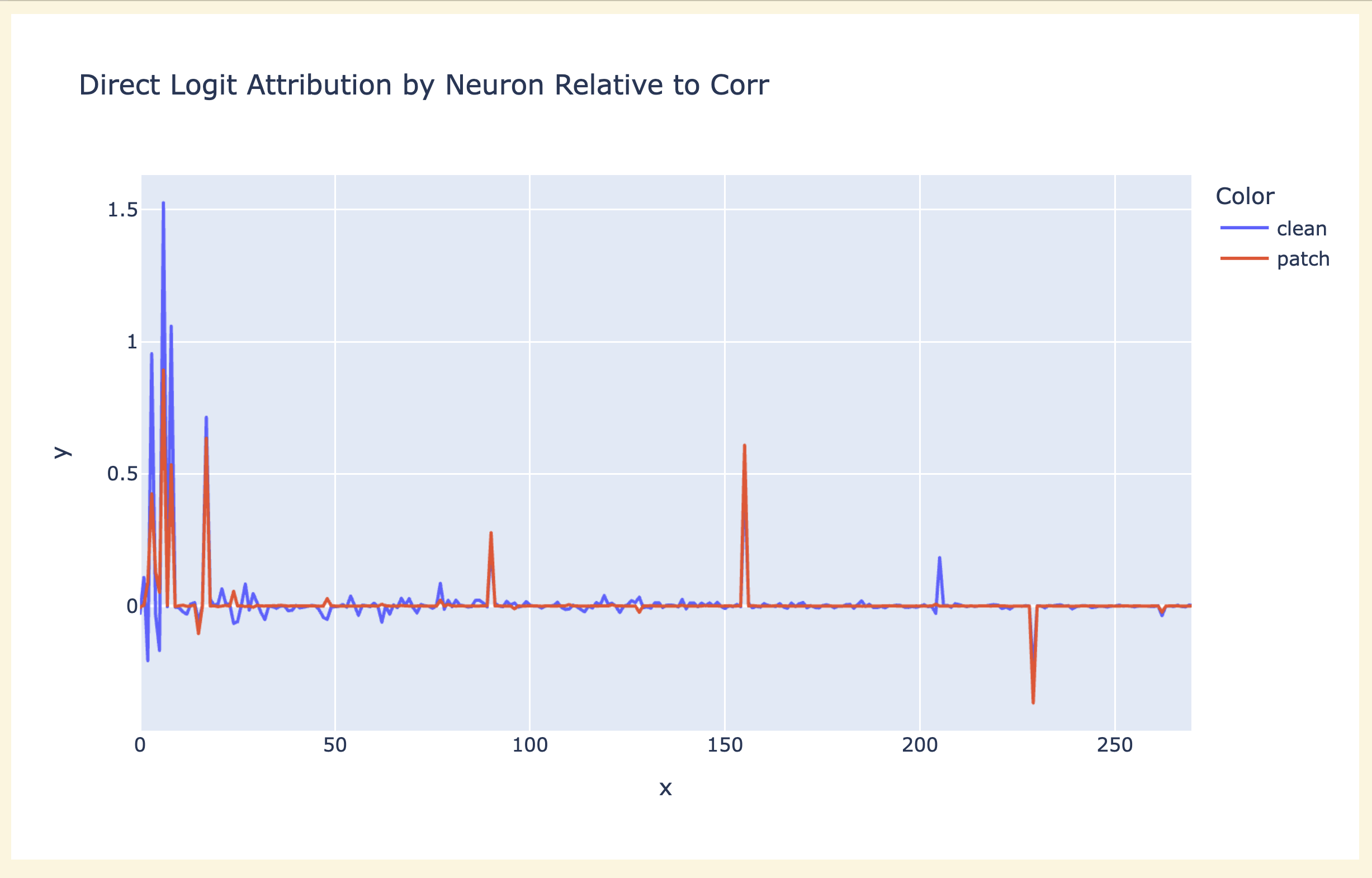
At this point I decided to pivot to just trying to interpret neuron L5N1393 itself, because it seemed interesting. And at this point I was pretty convinced that the model had interpretable (and maybe monosemantic?) neurons.

Looking at the direct logit attribution of the neuron, it strongly boosted C0 and slightly boosted D1 (one step diagonally down and right)

The next easiest place to start was max activating dataset examples - I initially felt an impulse to run the model across tens of thousands of games to collect the actual top dataset examples, but I realised this would be a headache and probably unnecessary. I had run the model for 50 games (thus 3000 moves) and decided to just inspect the neuron on the top 30 (1%) of games there.

I manually inspected a few, and then decided to aggregate the board state across the top 30 moves. I decided to try averaging "is non-empty", the actual board state (ie 1 for black, 0 for empty, -1 for white) and the flipped board state (ie 1 for mine, 0 for empty, -1 for their's) - this was kinda janky, since I wanted to distinguish "even probability of being white or black" and "always empty", but it seemed good enough to be useful.

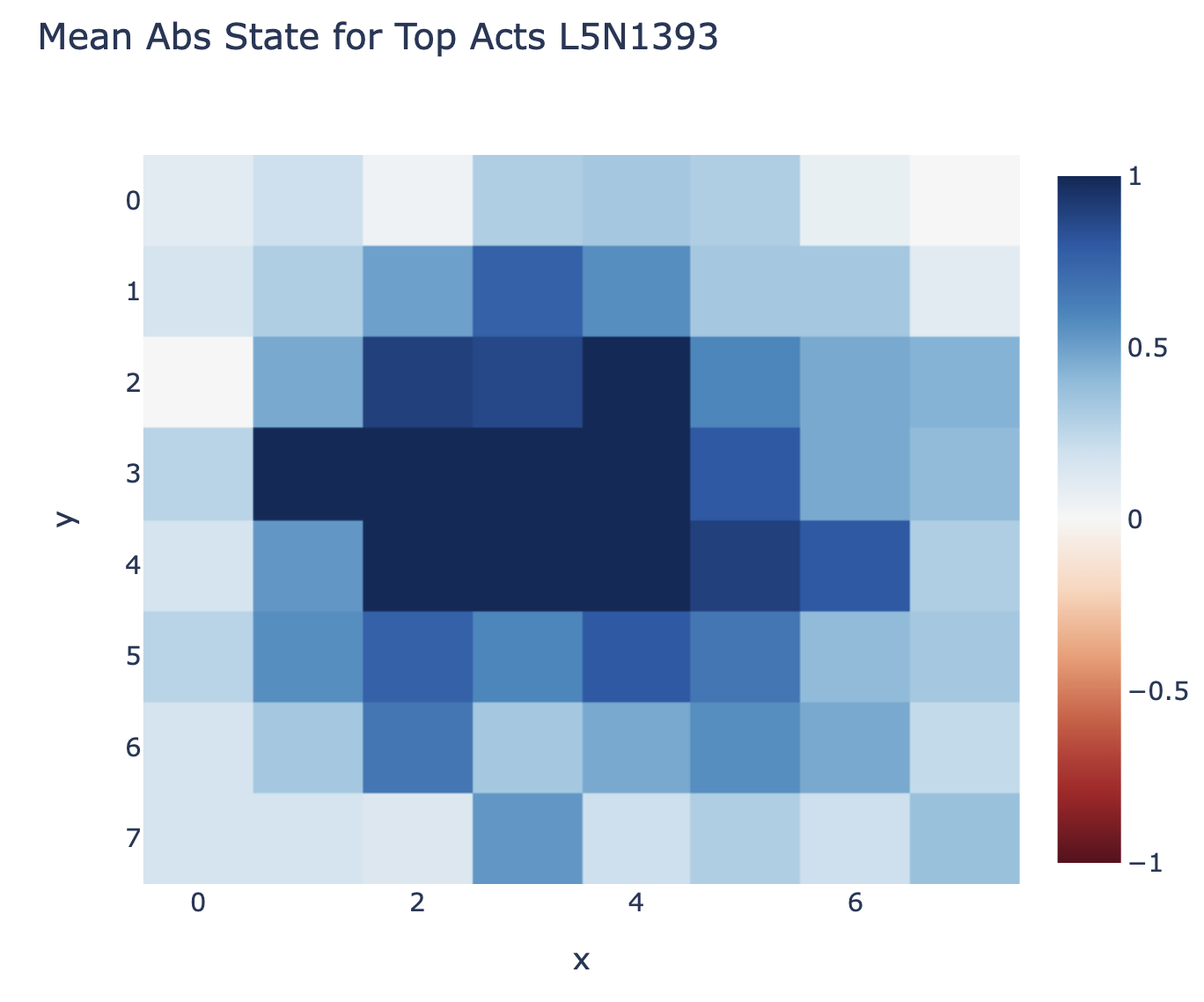
I don't recall exactly how I had the idea for a flipped board state - I think a combination of doing a heatmap of which games/moves the neuron fired on and seeing that it wasn't a consistent parity between games, but it did alternate within a game. And inspecting the top few examples, and seeing that some had black at D1 and white at E2, and some had white at D1 and black at E2 (and already having identified that part of the board as important). I spent a bit of time stuck on figuring out how best to aggregate a flipped board state, before realising I could do the stupid thing of using a for loop to generate an alternating tensor of 1s and -1s and just multiply by it.

But now I had the flipped board state, it was pretty clear that this was the right way to interpret the neuron - it was literally 1 in D1 and -1 in E2 (here 1 meant "their's", because I hadn't realised I'd need a good convention). I looked at the max activating dataset examples for a few other neurons (taking the top 10 by norm in each layer) and saw a few others that were clean in the flipped state but not in the normal state, and this was enough to generate the idea that the relevant colour was "next" vs "previous" player (I only realised after the fact that "my" vs "their" colour was a cleaner interpretation, thanks to Chris Olah for this!)

This is literally written in my notes as (immediately after I briefly decided to go and do a deep dive on neuron L6N1339 instead lol)

Omg idea! Maybe linear probes suck because it's turn based - internal repns don't actually care about white or black, but training the probe across game move breaks things in a way that needs smth non-linear to patch

At this point my instincts said to go and validate the hypothesis properly, look at a bunch more neurons, etc. But I decided that in the spirit of being decisive and pursuing "big if true" hypotheses (and because at this point I was late for work) I'd just say YOLO and try training a linear probe under this model.

I'm particularly satisfied with this decision, since I felt a lot of perfectionism, that I would have normally pursued, and ignoring it in the interests of speed went great:

  • I'd never trained a probe before, and figured there's a bunch of standard gotchas I needed to learn - eg how to deal with imbalanced class sizes (corners are normally empty), setting up good controls etc
  • Getting a probe working on the flipped board state (across all moves) - this seemed like more of a pain to code so I just decided to do even and odd moves
  • Figuring out the right layer to probe on - I just picked layer 6 since it was late enough to feel safe, and I didn't want to spend time figuring out the right layer to probe on
  • I had no idea what the right optimiser or hyper-parameters for training a probe are (I just guessed AdamW with lr=1e-4,wd=1e-2,b1=0.9,b2=0.99 and batch size 100 which seemed to work)
  • Getting accuracy to work for the probe was a headache (it involved a bunch of fiddling with one hotting the state in the right way)
  • Getting good summary statistics of how the run was going - I decided to just have overall loss per probe, and then loss per probe on an arbitrary square (I think C2)
  • Figuring out how to get good performance on probe training - there's a bunch of optimisations around stopping the model once it gets to the right layer, turning off autodiff on the model parameters, etc, I just decided to not bother and do the simple thing that should work.

I somehow managed to write training code that was bug free on the first long training run, and could see from the training curves that my probes were obviously working! From here on, things felt pretty clear, and I found the results in the initial section on analysing the probe!

Citation Info

Please cite this work as eg (if you have takes on how to properly cite blog posts, hit me up):

@misc{nanda_othello_2023, title={Actually, Othello-GPT Has A Linear Emergent World Model}, url={<https://neelnanda.io/mechanistic-interpretability/othello>}, journal={neelnanda.io}, author={Nanda, Neel}, year={2023}, month={Mar}}

$\setCounter{0}$
Neel Nanda
Previous

Tiny Mech Interp Projects: Emergent Positional Embeddings of Words
Next

Paper Replication Walkthrough: Reverse-Engineering Modular Addition